Pb1.mw
| > |
restart:r:=1/(1+e*cos(theta));De:=[1/e,t,t=-infinity..infinity]:Ce:=[r,theta,theta=-2*Pi..2*Pi]: Equation polaire de la conique |

Exercice 1: ici e=2
| > |
e:=2;plot(subs(e=2,Ce),-1..2,-2..2,coords=polar); |
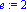
![[Plot]](images/Pb1_3.gif)
Exercice 3 a: ici e est quelconque
Warning, the protected names norm and trace have been redefined and unprotected
| > |
u:=vector([cos(theta),sin(theta)]);v:=vector([-sin(theta),cos(theta)]); voici les vecteurs de base du repère polaire (coordonnées dans le repere (F,i,j) |
![u := vector([cos(theta), sin(theta)])](images/Pb1_4.gif)
![v := vector([-sin(theta), cos(theta)])](images/Pb1_5.gif)
| > |
f:=scalarmul(u,r); voici la représentation paramétrique de la conique (le vecteur r*u(theta) |
![f := vector([cos(theta)/(1+e*cos(theta)), sin(theta)/(1+e*cos(theta))])](images/Pb1_6.gif)
| > |
fp:=map(diff,f,theta); voici le vecteur vitesse |
![fp := vector([cos(theta)*e*sin(theta)/(1+e*cos(theta))^2-sin(theta)/(1+e*cos(theta)), sin(theta)^2*e/(1+e*cos(theta))^2+cos(theta)/(1+e*cos(theta))])](images/Pb1_7.gif)
![fp := vector([-sin(theta)/(1+2*e*cos(theta)+e^2*cos(theta)^2), (cos(theta)+e)/(1+2*e*cos(theta)+e^2*cos(theta)^2)])](images/Pb1_8.gif)
| > |
t:=matadd(u,v,e*sin(theta),1+e*cos(theta)):vecteur t(theta) exprimé dans le repère (F,i,j) (matadd calcul la combinaison linéaire) |
![t := vector([-sin(theta), cos(theta)+e])](images/Pb1_9.gif)
| > |
Determinant:=det(matrix([fp,t])); On verifie bien que t et le vecteur vitesse sont colinéaires |

| > |
X:='X':Y:='Y':Ppol:=vector([X,Y]); On pose X,Y les coordonées de P dans la base R(theta); |
![Ppol := vector([X, Y])](images/Pb1_11.gif)
| > |
tpol:=vector([e*sin(theta),1+e*cos(theta)]); Il s'agit la des coordonnées de t dans le repère R(theta) |
![tpol := vector([e*sin(theta), 1+e*cos(theta)])](images/Pb1_12.gif)
| > |
eq_1:=dotprod(Ppol,tpol,orthogonal)=0; Cette équation exprime le fait que t et FP sont orthogonaux (donc de produit scalaire nul) |
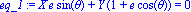
| > |
MPpol:=matadd(Ppol,[r,0],1,-1); vecteur MP en coordonnées polaires |
![MPpol := vector([X-1/(1+e*cos(theta)), Y])](images/Pb1_14.gif)
| > |
eq_2:=det(matrix([MPpol,tpol]))=0; Cette équation exprime le fait que P appartient à la tangente et donc MP est colinéaire à t. |
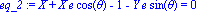
| > |
Sol:=simplify(solve({eq_1,eq_2},{X,Y})); On résout le système de ces deux équations |

| > |
X:=subs(Sol,X);Y:=subs(Sol,Y); D'où les coordonnées X.Y du projeté orthogonal |


D'où les coordonnées de P dans le repère (F,i,j)
| > |
P:=matadd(u,v,Ppol[1],Ppol[2]): |
![P := vector([(cos(theta)+e)/(1+2*e*cos(theta)+e^2), sin(theta)/(1+2*e*cos(theta)+e^2)])](images/Pb1_19.gif)
| > |
x1:=simplify(x);y1:=simplify(y); d'où l'équation paramétrée en x1,y1 |
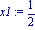
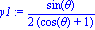
| > |
x1:=subs(theta=2*t,x1);y1:=subs(theta=2*t,y1); D'où en paramétrant par l'arc-moitié theta=2t |

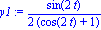
| > |
y1 := 1/2*sin(2*t)/(cos(2*t)+1): |
| > |
y1:=expand(y1); Ce qui se simplifie pour y1 |
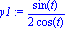
| > |
On voit donc que y parcourt tous les réels lorsque theta (i.e 2t) parcourt l'ensmble des réels |
il s'agit donc de la droite d'équation x=1/2
| > |
D1:=plot(subs(e=1,De),color=red): Directrice (en rouge) |
| > |
C1:=plot(subs(e=1,Ce),-1..1,-2..2,coords=polar,color=blue): conique (en bleu) |
| > |
Gamma1:=plot([1/2,t,t=-infinity..infinity],color=black): Gamma1 en noir |
Warning, the name changecoords has been redefined
![[Plot]](images/Pb1_25.gif)
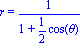
| > |
A:=simplify(subs(theta=0,[r*cos(theta),r*sin(theta)]));Ap:=simplify(subs(theta=Pi,[r*cos(theta),r*sin(theta)])); A et A' sont les points de paramètres 0 et Pi |
![A := [2/3, 0]](images/Pb1_27.gif)
![Ap := [-2, 0]](images/Pb1_28.gif)
| > |
Oo:=matadd(vector(A),vector(Ap),1/2,1/2); O est le milieu de [AA'] |
![Oo := vector([(-2)/3, 0])](images/Pb1_29.gif)
Comme A et A' appartiennent à Gamma1/2 (En effet les tangentes y sont perpendiculaires à l'axe focal) son centre appartient à la médiatrice x=-2/3
Par ailleurs cette ellipse étant symétrique par rapport à l'axe focal: (l'axe des s abscisses) il en va de même pour le cercle Gama1/2
son centre est donc sur l'axe des abscisses
D'où ses coordonnées (-2/3,0)
| > |
('x'+2/3)^2+'y'^2=simplify((x+2/3)^2+y^2); On trouve en remplacant x et y par son expression |
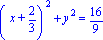
Il s'agit bien d'un cercle dont le rayon est 4/3
| > |
D2:=plot(subs(e=1/2,De),color=red): Directrice (en rouge) |
| > |
C2:=plot(subs(e=1/2,Ce),-2..2,-2..2,coords=polar,color=blue): conique (en bleu) |
| > |
Gamma2:=plot([x,y,theta=-2*Pi..2*Pi],color=black): Gamma1/2 en noir |
![[Plot]](images/Pb1_31.gif)
![]()
![]()
![[Plot]](images/Pb1_3.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Plot]](images/Pb1_25.gif)
![]()
![]()
![]()
![]()
![]()
![[Plot]](images/Pb1_31.gif)