| > | restart: |
Question a
| > | Limit(ln(cos(h))/(cos(h)-1),h=0)=limit(ln(cos(h))/(cos(h)-1),h=0); |
![]()
| > | Limit(sin(h)/h,h=0)=limit(sin(h)/h,h=0); |
![]()
| > | Limit(tan(h)/h,h=0)=limit(tan(h)/h,h=0); |
![]()
| > | Limit((1-cos(h))/h**2,h=0)=limit((1-cos(h))/h**2,h=0); |
![]()
| > |
| > | Question b |
| > | deriv_f:=diff(ln((tan(x))),x):Diff(ln((tan(x))),x)=deriv_f; la valeur absolue ne compte pas dans tout intervalle ou tan>0 |
![]()
| > | deriv_f:=simplify(convert(deriv_f,sin)):Diff(ln((tan(x))),x)=deriv_f; |
![]()
| > | deriv_f:=convert(deriv_f,sin):Diff(ln((tan(x))),x)=deriv_f; |
![]()
| > |
| > | Question c |
| > | E:=sin(2*t)*diff(y(t),t)-2*y(t)=sin(2*t); L'Equation Différentielle (E) |
![]()
| > | ER:=expand(E/sin(2*t)); Equation résolue |
![]()
| > | ER:=convert(ER,sin); |
![]()
| > | EHR:=lhs(ER)=0; Equation homogène résolue |
![]()
| > |
| > | On reconnait une eq diff du premier ordre y'+ay=0 avec a(t)=2/sin(2t) dont une primitive est d'après ce qui prècède ln(|tan t|) |
| > | y0:=rhs(dsolve(EHR)): |
| > | y0:=expand(convert(y0,tan)):y0:=expand(y0); Solution générale de l'Equation Homogène résolue |
![]()
| > |
Ceci est conforme à nos attentes, Utilisons la méthode de la variation de la constante pour déterminer une solution de ER
| > | y0:=subs(_C1=1,y0): |
| > | Y:=lambda(t)*y0; |
![]()
| > | Evc:=subs(y(t)=Y,ER): On injecte Y dans l'équation E |
| > | EvC:=simplify(Evc); lambda est solution de l'équation |
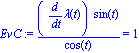
D'où lambda n'est autre qu'une primitive cotan
| > | lambda0:=rhs(dsolve(Evc)); |
![]()
D'où la solution générale de E
| > | Y:=lambda0*y0; |
![]()
| > |
| > | Question d |
si la solution existe en 0, neccessairement y(0)=0 en effet
| > | simplify(subs(t=0,E)); |
![]()
Et par continuité y(0)=0=limite de Y en 0, or
| > | Limit(Y,t=0,right)=limit(Y,t=0,right); |
![]()
Cette solution est compatible pour la continuité vérifions pour la dérivabilité, en regardant la limite du taux d'accroissemnt en 0
| > | Limit(('Y(t)'-'Y(0)')/t,t=0,right)=limit(Y/t,t=0,right); |
![]()
D'où pas de solution sur [0,Pi/2[
| > |
| > | Question e |
Si solution il y a sur ]0,Pi[ elle doit correspondre à deux solutions sur ]0,Pi/2[ et sur ]Pi/2,Pi[ qui se racordent de facon dérivable en Pi/2
| > | y1:=subs(_C1=A,Y); solution sur ]0,Pi/2[ |
![]()
| > | y2:=subs(_C1=B,Y); solution sur ]Pi/2,Pi[ |
![]()
Vérifions si le raccordement peut être continu
| > | Limit('y1(t)',t=Pi/2,left)=limit(y1,t=Pi/2,left); |
![]()
| > | Limit('y2(t)',t=Pi/2,left)=limit(y2,t=Pi/2,left); |
![]()
D'où nécessairement A=B=0
| > | y1:=subs(A=0,y1);y2:=subs(B=0,y2); |
![]()
![]()
Et dans ce cas y s'obtient par prolongement par continuité puisque
| > | Limit('y1(t)',t=Pi/2,left)=limit(y1,t=Pi/2,left);Limit('y2(t)',t=Pi/2,right)=limit(y2,t=Pi/2,right); |
![]()
![]()
D'où nécessairement y(0)=0
Vérifions si ce prolongement est dérivable, en regardant la limite du taux d'accroissemnt en 0
| > | Limit(('y(t)'-'y(0)')/(t-Pi/2),t=Pi/2)=limit(y1/(t-Pi/2),t=Pi/2); |
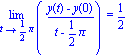
C'est le cas!!!!
| > |
Vérifions ce que dit Maple
| > | dsolve(E,y(t)); |
![]()
| > |