| > | restart: |
trajectoire elliptique
| > | r:=theta->p/(1-e*cos(theta-theta0)); |
![]()
| > |
Exercice 1
Calcul de e^2 et cos^2(theta0) en fonction de p,R et du demi grand axe a
| > |
| > | ra:=r(theta0); apogée |
![]()
| > | rp:=r(theta0+Pi); périgée |
![]()
| > | eq_a:=2*a=rp+ra; Equation du demi-grand axe |
![]()
| > | eq_R:=R=r(0); Condition initiale du tir |
| > |
![]()
On resout le systeme composée des deux égalités précendentes pour les inconnues e et cos(theta0)
| > | sol:=solve({eq_a,eq_R},{e,cos(theta0)}); |
![]()
| > | sol:=allvalues(sol);on explicite l'expression de e à l'aide de la fonction allvalues |
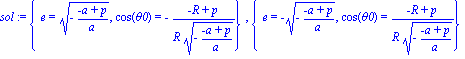
| > | sol_part:=[op(sol[1])];on ne garde que que la solution vérifiant e>0 |
![sol_part := [e = (-(-a+p)/a)^(1/2), cos(theta0) = -(-R+p)/(R*(-(-a+p)/a)^(1/2))]](images/Kh04_8.gif)
| > | edeux:=subs(sol_part,e)^2;on calcule e^2 |
![]()
| > | costheta0deux:=subs(sol_part,cos(theta0))^2;on calcule cos(theta0)^2 |
![]()
| > |
Exercice 2
| > |
Constante de la loi des aires: conservation du moment cinétique
| > | C:=R*v0*sin(alpha); |
![]()
Expression de p en fonction des conditions initiales
| > | p:=C*C/(G*M); |
![]()
| > | p:=subs(G=vc*vc*R/M,p); injectons dans p l'expression de G |
![]()
| > | p:=subs(v0=T*vc,p); injectons dans p l'expression de v0=T*vc |
![]()
| > |
| > | Exercice 3 |
| > |
Expression de la conservation de l'énergie mécanique
| > | eq_E:=(1/2)*m*v0*v0-G*M*m/R=-G*M*m/(2*a); |
![]()
| > | a:=solve(eq_E,a); expression de a |
![]()
| > | a:=subs(G=vc*vc*R/M,a); injectons dans a l'expression de G |
![]()
| > | a:=subs(v0=T*vc,a); injectons dans a l'expression de v0 |
![]()
| > | a:=simplify(a); on simplifie l'expression |
![]()
| > | Exercice 4 |
| > |
Etude de la portée
| > | costheta0deux;costheta0deux:=subs(sin(alpha)^2=1-cos(alpha)^2,costheta0deux); expression de cos(theta0)^2 en fonction de cos(alpha)^2 |


Calcul des extrema
| > | ct2:=subs(cos(alpha)^2=x,costheta0deux);expression de cos(theta0)^2 en fonction de x=cos(alpha)^2 |

| > | deriv:=diff(ct2,x); dérivée par rapport à x |

| > | sol:=solve(deriv=0,x); recherche des valeurs critiques |
![]()
| > | cos_carre_alpha_optimum_1:=sol[1];cos_carre_alpha_optimum_2:=sol[2]; expression des valeurs optimales de cos(alpha)^2 |
![]()
![]()
Il s'agit bien d'un maximum de theta0 et donc un minimum de cos(theta0)^2 pour cos_carre_optimum_2 (seule valeur acceptable)
| > | delta:=factor(ct2-subs(x=cos_carre_alpha_optimum_2,ct2)); expression de la difference cos(theta0(x))^2-cos(theta0(xoptimum))^2 |

| > | assume(x>0 and x<1);assume(T>0 and T<1); is(delta>=0);cette différence est bien positive |
![]()
| > |
| > |
| > | Exercice 5 |
| > |
Application Numérique
| > | R:=6400000;T:=0.99;'cos_carre_alpha_optimum_2'=cos_carre_alpha_optimum_2; |
![]()
![]()
![]()
| > | Digits:=3:alpha:=arccos(sqrt(cos_carre_alpha_optimum_2));theta0:=arccos(sqrt(costheta0deux)); |
![]()
![]()
| > | 'p'=p;e:=sqrt(edeux);'r(theta)'=r(theta); |
![]()
![]()
![]()
| > | with(plots): |
Warning, the name changecoords has been redefined
| > | terre:=plot([R,theta,theta=0..2*Pi],coords=polar,scaling=constrained,color=blue,thickness=3): |
| > | traj:=plot([r(theta),theta,theta=0..2*theta0],coords=polar,scaling=constrained,color=red,thickness=2): |
| > | display(terre,traj); |
![[Plot]](images/Kh04_37.gif)
| > | fleche=(ra-R)/1000; hauteur de la flècehe de la trajectoire relativement à la surface terrestre en km |
![]()