>	restart;with(plots):alpha:=0:Digits:=30:

Warning, the name changecoords has been redefined

>

Exercice 4

>

>	epsilon:=10^(-9):seuil:=10:phi:=x->-ln(abs(x+epsilon))+seuil: Fonction atténuant la dispersion des points calculés

>

>

>	Premier exemple

>

>

>	f:=x->(exp(-0.5*x))-1;a:=-4;b:=5;N:=80;c0:=5;r0:=5;

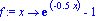
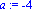
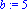
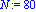
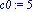
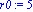
>	sD:=evalf(Dichotomie(f,a,b,N)):sC:=Cauchy(f,c0,N):sN:=Newton(f,r0,N):

>	pD:=[seq([i,phi(sD[i])],i=1..N)]:pC:=[seq([i,phi(sC[i])],i=1..N)]:pN:=[seq([i,phi(sN[i])],i=1..N)]:

>	plot([pD,pC,pN],0..N,color=[black,blue,red],style=point,thickness=2);

En noir les points calculés par la méthode de dichotomie
En bleu les points calculés par la méthode de point fixe de Cauchy-Picard
En rouge es points calculés par la méthode de Newton-Raphson

>

>

>	Deuxième exemple

>

>

>	f:=x->(exp(-x/1000))-x-1;a:=-150;b:=100;N:=80;c0:=10;r0:=10;

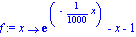
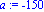
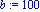
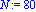
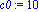
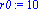
>	sD:=evalf(Dichotomie(f,a,b,N)):sC:=Cauchy(f,c0,N):sN:=Newton(f,r0,N):

>	pD:=[seq([i,phi(sD[i])],i=1..N)]:pC:=[seq([i,phi(sC[i])],i=1..N)]:pN:=[seq([i,phi(sN[i])],i=1..N)]:

>	plot([pD,pC,pN],0..N,color=[black,blue,red],style=point,thickness=2);

En noir les points calculés par la méthode de dichotomie
En bleu les points calculés par la méthode de point fixe de Cauchy-Picard
En rouge es points calculés par la méthode de Newton-Raphson

>

>

>	Troisième exemple

>

>

>	f:=x->sinh(x/10^4)/10^(-20);a:=-5*10^3;b:=10^4;N:=80;c0:=9*10^3;r0:=9*10^3;

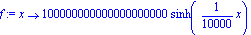
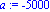
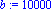
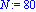
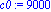
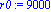
>	sD:=Dichotomie(f,a,b,N):sC:=Cauchy(f,c0,N):sN:=Newton(f,r0,N):

>	pD:=[seq([i,phi(sD[i])],i=1..N)]:

>	pC:=[seq([i,phi(sC[i])],i=1..N)]:

>	pN:=[seq([i,phi(sN[i])],i=1..N)]:

>	plot([pD,pC,pN],0..N,color=[black,blue,red],style=point,thickness=2);

En noir les points calculés par la méthode de dichotomie
En bleu les points calculés par la méthode de point fixe de Cauchy-Picard
En rouge es points calculés par la méthode de Newton-Raphson

>

Conclusion

Les méthodes Dichotomie et Point fixe ont des points dont les logarithmes sont distribués linéairement (pente identique pour la dichotomie, pente variable pour la méthode du point fixe)
En revanche la méthode de NEwton-Raphson semble répartir ces logarithmes suivant une parabole (elle est donc plus rapide à atteindre sa valeurs seuil) on dit qu'il s'agit d'une méthode quadratique.

>