Newton.mw

> restart;with(plots):secu:=50:secu est un nombre maximal d'itérations, évitant les boucles trop longues

Warning, the name changecoords has been redefined

Exercice 3

>

Questions a) et b)

> impact:=(f,a)->a-f(a)/D(f)(a);

impact := proc (f, a) options operator, arrow; a-f(a)/D(f)(a) end proc

> Newton:=proc(f,a,epsilon)
local aa,bb,compteur,milieu,suite_m;
aa:=a;bb:=impact(f,aa);compteur:=1;
while is(abs(bb-aa)>epsilon) and is(compteur<secu) do
compteur:=compteur+1;aa:=bb;bb:=impact(f,bb);
od;
[compteur,aa];
end:

>

Question c)

Premier exemple

> f:=x->x^3-4*x+1;a:=-2;epsilon:=10^(-9);

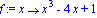
f := proc (x) options operator, arrow; x^3-4*x+1 end proc

a := -2

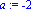
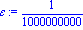
epsilon := 1/1000000000

> sol:=evalf(Newton(f,a,epsilon)); solution proposé par la procédure Newton

sol := [5., -2.114907541]

> 'f'(sol[2])=evalf(f(sol[2])); valeur de f en ce point

f(-2.114907541) = 0.4e-8

>

>

>

Deuxième exemple

> f:=x->x^3-4*x+1;a:=0;epsilon:=10^(-9);

f := proc (x) options operator, arrow; x^3-4*x+1 end proc

a := 0

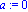
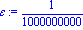
epsilon := 1/1000000000

> sol:=evalf(Newton(f,a,epsilon)); solution proposé par la procédure Newton

sol := [4., .2541016884]

> 'f'(sol[2])=evalf(f(sol[2])); valeur de f en ce point

f(.2541016884) = -0.1e-8

>

Troisième exemple

> f:=x->x^3-4*x+1;a:=2;epsilon:=10^(-9);

f := proc (x) options operator, arrow; x^3-4*x+1 end proc

a := 2

epsilon := 1/1000000000

> sol:=evalf(Newton(f,a,epsilon)); solution proposé par la procédure Newton

sol := [5., 1.860805853]

> 'f'(sol[2])=evalf(f(sol[2])); valeur de f en ce point

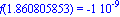
f(1.860805853) = -0.1e-8

>

Illustration Graphique

>

> f:=x->exp(-x*x/2)-1/2;a:=0.3;epsilon:=10^(-2);

f := proc (x) options operator, arrow; exp(-x*x*1/2)-1/2 end proc

a := .3

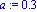
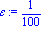
epsilon := 1/100

> sol:=SNewton(f,a,epsilon):

> N:=sol[1]:s:=sol[2..N+1]:

> Graphique(f,0,2,N,s);

[Plot]

>

>

> sur l'axe des abbscissdes apparaissent les points de la suite x(n+1)=impact(xn,f)
la courbe est cell de f

> points:=seq([i,s[i]],i=1..N):

> plot([points],color=black,thickness=2,style=point);

[Plot]

>

>

>

>

>

>

> Les points tracés sont ceux de coordonnées (n,xn)

>

> Un phénomène cyclique

> f:=x->x*(x^2-16)/20;a:=4/sqrt(5);epsilon:=1:

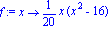
f := proc (x) options operator, arrow; 1/20*x*(x^2-16) end proc

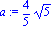
a := 4/5*5^(1/2)

> sol:=SNewton(f,a,epsilon):

> N:=sol[1]:s:=sol[2..N+1]:

> Graphique(f,-2,2,N,s);

[Plot]

> Quelques explications.

>

Que ce soit dans la méthode de Cauchy-Picard ou celle de Newton-Raphson, il s'agit d'approcher les solutions par une suite du type u(n+1)=g(un)

>

Comme on l'a vu dans le cas du point fixe de Cauchy-Picard, une petite valeur de la constant k, permet d'assurer le caractère contractant de g:x->x-kf(x) (au moins localement) en particulier si |f'| est petit la méthode de Cauchy-Picard semble adapté. En revanche des grandes valeurs de f' peuvent faire craindre la perte du caractère contractant

Dans le cas Newton-Raphson, la constante k devient varaible (et s'adapte d'autant mieux au choix de f, qu'il s'agit de f') g:x->x-f(x)/f'(x)... Ici c'est lorsque |f'| est grand (courbe très pentue) que la méthode est d'autant plus efficace. En revanche plus la dérivée est petite (pente quasi-horizontale) plus le point d'impact s'eloigne dangeruesement de la solution.