exo4.mw

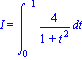
Exercice 4

> restart:Digits:=30:with(plots):with(plottools):

> fI:=t->4/(1+t^2):aI:=0:bI:=1:NI:=20:

> fJ:=t->exp(-t*t):aJ:=-10:bJ:=10:NJ:=20:

>

Question a)

> Rectangle_m:=proc(f,a,b,N)
local i,S;
S:=0;
for i from 0 to N-1 do
S:=S+f(a+(i+1/2)*(b-a)/N);
od;
S:=S*(b-a)/N;
end:

>

> Question b)

Calcul approché de I avec 20 Rectangles où

> I=Int(fI(t),t=aI..bI);

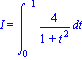
I = Int(4/(1+t^2), t = 0 .. 1)

> I_(approché):=evalf(Rectangle_m(fI,aI,bI,NI));

I_(approché) := 3.14180098689309349196826100544

> erreur:=evalf(abs(I_(approché)-Pi));

erreur := 0.20833330330025350561762216e-3

>

Calcul approché de J avec 20 Rectangles où

> J=(Int(fJ(t),t=aJ..bJ))**2;

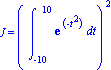
J = (Int(exp(-t^2), t = -10 .. 10))^2

> J_(approché):=evalf((Rectangle_m(fJ,aJ,bJ,NJ))**2);

J_(approché) := 3.14094271448126110962795947376

> erreur:=evalf(abs(J_(approché)-Pi));

erreur := 0.64993910853212883468390952e-3

>

> Question c)

> Points_Rm:=proc(f,a,b,N)
local i,S;
S:=NULL;
for i from 1 to N do S:=S,[i/N,Rectangle_m(f,a,b,i)]; od;
[S];
end;

>

Points_Rm := proc (f, a, b, N) local i, S; S := NULL; for i to N do S := S, [i/N, Rectangle_m(f, a, b, i)] end do; [S] end proc

> plot(Points_Rm(fI,aI,bI,50)); Tracé des points obtenus pour le calcul approché de I

[Plot]

> plot(Points_Rm(fJ,aJ,bJ,50)); Tracé des points obtenus pour le calcul approché de J

[Plot]

>

> Question d)

> Suite_Rm:=proc(f,a,b,N)
local i,S,suite,delta;
delta:=(b-a)/N;S:=NULL;
for i from 0 to N-1 do
S:=S,polygon([[a+i*delta,0],[a+(i+1)*delta,0],[a+(i+1)*delta,f(a+(i+1/2)*delta)],[a+i*delta,f(a+(i+1/2)*delta)]],color=green,thickness=2);
od;
S;
end:

>

Tracé des rectangels correspondant à l'intégrale I

> RmI:=Suite_Rm(fI,aI,bI,NI):GI:=plot(fI,aI..bI,color=black,thickness=3):

> plots[display](RmI,GI);

[Plot]

Tracé des rectangels correspondant à l'intégrale J

> RmJ:=Suite_Rm(fJ,aJ,bJ,NJ):GJ:=plot(fJ,aJ..bJ,color=black,thickness=3):

> plots[display](RmJ,GJ);

[Plot]

>

Une petite animation

>

> Anim_Rm:=proc(t) plots[display](GI,Suite_Rm(fI,aI,bI,trunc(t))); end:

> animate(Anim_Rm,[t],t=1..NI, frames=50);

[Plot]

>

>