| > | Exercice 6-bis |
![]()
| > | restart:Digits:=30: |
![]()
![]()
![]()
![]()
| > | restart:Digits:=30:N:=100: |
Grace à l'inégalité de Taylor-Lagrange
| > | abs(f(b) -Sum(Diff(f(a),t$k)/(k!)*(b-a)^k,k=0..'N'))<=sup(abs(Diff(f(t),t$(k+1))))/((n+1)!)*(b-a)^(n+1); |
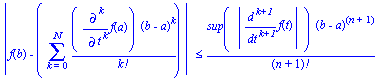
On etudie donc la suite de Taylor (Taylor_n) associée à la fonction t->4/(1+t^2)
| > | Taylor[n]:=Sum(Diff(f(a),t$k)/(k!)*(b-a)^k,k=0..'N')=Taylor[n-1]+Diff(f(a),t$k)/(n!)*(b-a)^n; |
![Taylor[n] := Sum((Diff(f(a), `$`(t, k)))*(b-a)^k/factorial(k), k = 0 .. N) = Taylor[n-1]+(Diff(f(a), `$`(t, k)))*(b-a)^n/factorial(n)](images/exo6bis_7.gif)
| > | Taylor:=proc(f,a,b,N) options remember;
local S; if N=0 then S:=f(a); else S:=((D@@N)(f))(a)*(b-a)^N/N!+Taylor(f,a,b,N-1); fi; S; end: |
| > |
| > |
Appliquons ceci à la fonction arctan entre 0 et 1 pour N=100 tels que ci-dessous
| > | f:=t->arctan(t);a:=0;b:=1;N:=100; |
| > |
| > | for i from 0 to N do 4*Sum(((D@@k)(f))(a)*(b-a)^k/k!,k=0..i)=4*Taylor(f,a,b,i), erreur=evalf(4*Taylor(f,a,b,i)-Pi); od; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > |
| > |