| > | restart;
|
| > | with(linalg); |
Warning, the protected names norm and trace have been redefined and unprotected
![]()
![]()
![]()
![]()
Résolution d'un système
| > | A:=array(1..4,1..4): for i from 1 to 4 do for j from 1 to 4 do A[i,j]:=i+j: od:od: |
| > | A=evalm(A); |
![A = matrix([[2, 3, 4, 5], [3, 4, 5, 6], [4, 5, 6, 7], [5, 6, 7, 8]])](images/Gauss_5.gif)
| > | Gsyst(A,[x,y,z,t],[6,7,8,9]); |

![L[1],](images/Gauss_7.gif)
![L[2],](images/Gauss_8.gif)
![L[3],](images/Gauss_9.gif)
![L[4],](images/Gauss_10.gif)
![L[2],](images/Gauss_11.gif)
![L[3],](images/Gauss_12.gif)
![L[4],](images/Gauss_13.gif)
![C[3],](images/Gauss_14.gif) ", C[4], matrix([[x, 3/2*y, 5/2*t, 2*z], [0, y, 3*t, 2*z], [0, 0, 0, 0], [0, 0, 0, 0]]), "=", matrix([[3], [4], [0], [0]])" align="center">
", C[4], matrix([[x, 3/2*y, 5/2*t, 2*z], [0, y, 3*t, 2*z], [0, 0, 0, 0], [0, 0, 0, 0]]), "=", matrix([[3], [4], [0], [0]])" align="center">
![]()
![]()
![]()
![]()
![]()

![]()
| > | Calcul du rang |
| > | A:=array(1..4,1..4): for i from 1 to 4 do for j from 1 to 4 do A[i,j]:=min(i-1,j-1): od:od: |
| > | A=evalm(A); |
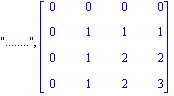
![A = matrix([[0, 0, 0, 0], [0, 1, 1, 1], [0, 1, 2, 2], [0, 1, 2, 3]])](images/Gauss_22.gif)
| > | Grang(A); |
![C[1],](images/Gauss_24.gif) ", C[2], matrix([[0, 0, 0, 0], [1, 0, 1, 1], [1, 0, 2, 2], [1, 0, 2, 3]])" align="center">
", C[2], matrix([[0, 0, 0, 0], [1, 0, 1, 1], [1, 0, 2, 2], [1, 0, 2, 3]])" align="center">
![L[2],](images/Gauss_25.gif) ", L[1], matrix([[1, 0, 1, 1], [0, 0, 0, 0], [1, 0, 2, 2], [1, 0, 2, 3]])" align="center">
", L[1], matrix([[1, 0, 1, 1], [0, 0, 0, 0], [1, 0, 2, 2], [1, 0, 2, 3]])" align="center">
![L[3],](images/Gauss_26.gif)
![L[4],](images/Gauss_27.gif)
![C[2],](images/Gauss_28.gif) ", C[3], matrix([[1, 1, 0, 1], [0, 0, 0, 0], [0, 1, 0, 1], [0, 1, 0, 2]])" align="center">
", C[3], matrix([[1, 1, 0, 1], [0, 0, 0, 0], [0, 1, 0, 1], [0, 1, 0, 2]])" align="center">
![L[3],](images/Gauss_29.gif) ", L[2], matrix([[1, 1, 0, 1], [0, 1, 0, 1], [0, 0, 0, 0], [0, 1, 0, 2]])" align="center">
", L[2], matrix([[1, 1, 0, 1], [0, 1, 0, 1], [0, 0, 0, 0], [0, 1, 0, 2]])" align="center">
![L[4],](images/Gauss_30.gif)
![C[3],](images/Gauss_31.gif) ", C[4], matrix([[1, 1, 1, 0], [0, 1, 1, 0], [0, 0, 0, 0], [0, 0, 1, 0]])" align="center">
", C[4], matrix([[1, 1, 1, 0], [0, 1, 1, 0], [0, 0, 0, 0], [0, 0, 1, 0]])" align="center">
![L[4],](images/Gauss_32.gif) ", L[3], matrix([[1, 1, 1, 0], [0, 1, 1, 0], [0, 0, 1, 0], [0, 0, 0, 0]])" align="center">
", L[3], matrix([[1, 1, 1, 0], [0, 1, 1, 0], [0, 0, 1, 0], [0, 0, 0, 0]])" align="center">
| > | Résolution d'un système de CRAMER |
| > | A:=array(1..4,1..4): for i from 1 to 4 do for j from 1 to 4 do A[i,j]:=min(i,j): od:od: |
| > | A=evalm(A); |
![A = matrix([[1, 1, 1, 1], [1, 2, 2, 2], [1, 2, 3, 3], [1, 2, 3, 4]])](images/Gauss_33.gif)
| > | Gsyst_cramer(A,[x1,x2,x3,x4],[y1,y2,y3,y4]); |

![L[2],](images/Gauss_35.gif)
![L[3],](images/Gauss_36.gif)
![L[4],](images/Gauss_37.gif)
![L[3],](images/Gauss_38.gif)
![L[4],](images/Gauss_39.gif)
![L[4],](images/Gauss_40.gif)
![L[1],](images/Gauss_41.gif)
![L[2],](images/Gauss_42.gif)
![L[3],](images/Gauss_43.gif)
![L[1],](images/Gauss_44.gif)
![L[2],](images/Gauss_45.gif)
![L[1],](images/Gauss_46.gif)
| > | Calcul de l'inverse d'une matrice |
| > | Ginverse(A); |
![matrix([[1, 1, 1, 1], [1, 2, 2, 2], [1, 2, 3, 3], [1, 2, 3, 4]]),](images/Gauss_47.gif)
![matrix([[1, 1, 1, 1], [0, 1, 1, 1], [1, 2, 3, 3], [1, 2, 3, 4]]), L[2],](images/Gauss_48.gif)
![matrix([[1, 1, 1, 1], [0, 1, 1, 1], [0, 1, 2, 2], [1, 2, 3, 4]]), L[3],](images/Gauss_49.gif)
![matrix([[1, 1, 1, 1], [0, 1, 1, 1], [0, 1, 2, 2], [0, 1, 2, 3]]), L[4],](images/Gauss_50.gif)
![matrix([[1, 1, 1, 1], [0, 1, 1, 1], [0, 0, 1, 1], [0, 1, 2, 3]]), L[3],](images/Gauss_51.gif)
![matrix([[1, 1, 1, 1], [0, 1, 1, 1], [0, 0, 1, 1], [0, 0, 1, 2]]), L[4],](images/Gauss_52.gif)
![matrix([[1, 1, 1, 1], [0, 1, 1, 1], [0, 0, 1, 1], [0, 0, 0, 1]]), L[4],](images/Gauss_53.gif)
![matrix([[1, 1, 1, 0], [0, 1, 1, 1], [0, 0, 1, 1], [0, 0, 0, 1]]), L[1],](images/Gauss_54.gif)
![matrix([[1, 1, 1, 0], [0, 1, 1, 0], [0, 0, 1, 1], [0, 0, 0, 1]]), L[2],](images/Gauss_55.gif)
![matrix([[1, 1, 1, 0], [0, 1, 1, 0], [0, 0, 1, 0], [0, 0, 0, 1]]), L[3],](images/Gauss_56.gif)
![matrix([[1, 1, 0, 0], [0, 1, 1, 0], [0, 0, 1, 0], [0, 0, 0, 1]]), L[1],](images/Gauss_57.gif)
![matrix([[1, 1, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]), L[2],](images/Gauss_58.gif)
![matrix([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]]), L[1],](images/Gauss_59.gif)
| > |