Exercice 2
On défnit la paramétrisation, puis on construit le support partiel et sir la totalité des paramètresOn défnit la paramétrisation, puis on construit le support partiel et sir la totalité des paramètres

>

restart;

>	x:=t->t/(t^2-1);y:=t->t^2/(t-1);

>	total:=[x(t),y(t),t=-infinity..infinity]:

>	plot(total);

Cherchons le points multiples

1ere Méthode

>	plot(x,-2..2,-10..10,discont=true);

On voit que x est impaire et que tout point image admet deux antécédents

>	tx:=solve(x(t)=u,t);

Vérifions si pour ces deux antécédents t1 et t2 d'un point image u de x, les images par y sont les mêmes

>	y1:=y(tx[1]);y2:=y(tx[2]);

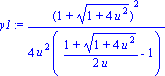
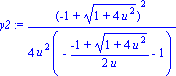
Calculons donc pour quelle valeur de u, les paramètres t1 et t2 ont mêmes images par y

>	solve(y1=y2,u);

seule la valeur réelle de u, convient, i.e. u=-1. Et donc on a un point double dont les paramètres sont

>	t_double:=solve(x(t)=-1,t);

il s'agit du point D de coordonnées

>	simplify([x(t_double),y(t_double)]);

Ainsi le point O de pamétre 0 est un point triple, les autres sont des points simples.

>

Tracons le support de la courbe autour de ce point double

>

>	plot(total,-5..5,-2..1);

Attention MAPLE semble détecter d'autres points multiples... Pourquoi???

2eme Méthode

Autre méthode: plutôt que partir des antécédents de x, prenons ceux de y

>	plot(y,-10..10,-10..10,discont=true);

là encore, on voit que tout point image admet deux antécédents

>	ty:=solve(y(t)=u,t);

Vérifions si pour ces deux antécédents t1 et t2 d'un point image u de y, les images par x sont les mêmes

>	x1:=x(ty[1]);x2:=x(ty[2]);

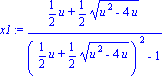
Calculons donc pour quelle valeur de u, les paramètres t1 et t2 ont mêmes image par x

>	solve(x1=x2,u);

Cependant, ici il y a un piège, en effet si u vaut 0 ou 4 Alors t1=t2 (voir expressions de ty) et donc il ne s'agit plus d'un point double, car le paramètre est le même

il ne reste donc que le cas u=-1, c'est à dire le point d'ordonnée -1 et pour paramètres

>	solve(y(t)=-1,t);

CQFD

3eme Méthode

Dernière Méthode (Le Meilleur pour la fin). Essayons sans trop de calcul de retrouver le résultat

Soient t1 et t2 deux paramètres distincts correspondants à un point double. Le couple (t1,t2) est un couple solution  du systéme

>	systeme:=[x(t1)-x(t2)=0,y(t1)-y(t2)=0];

On simplifie les expressions

>	systeme:=factor(systeme);

t1 est différent de t2 (on cherche un point double) et tous deux sont distincts de  1 (voir domaine de définition)

Donc ce système est équivalent au nouveau système

>	systeme_equiv:=(t2-1)*(t1-1)/(t1-t2)*systeme;

On met un peu d'ordre

>	systeme_equiv:=simplify(expand(systeme_equiv));

Multiplier la premiere composante par (t1+1)(t2+1) nous donne un deuxième systeme équivalent car t1 et t2 sont distincts de -1

>	Mult:=(a,b)->[(t1+1)*(t2+1)*a,b];

>	systeme_bis:=Mult(op(systeme_equiv));

Au lieu de résoudre ce système en t1 et t2 nous allons le résoudre pour les inconnues p=t1*t2 et s=t1+t2

>	Sps:=subs(t2*t1=p,t1=s-t2,systeme_bis);

On change la structure de liste en structure d'ensemble

>	Sps:={op(Sps)};

>	solve(Sps);

Et donc connaissant le produit p et la somme s, on sait que t1 et t2 sont les deux racines distinctes de X^2-sX+p=X^2+X-1... CQFD

>

4eme Méthode

#Dernière Méthode (promis c'est vraiment la dernière): On laisse MAPLE tout faire

>	systeme:={x(t1)-x(t2)=0,y(t1)-y(t2)=0};

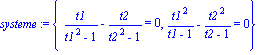
>	reponse:=[solve(systeme)];

On exclut bien sur les solutions correspondants à des paramètres identiques (on veut des points DOUBLES);

>	allvalues(reponse);

>