Exercice 9

On défnit la paramétrisation,

>

restart;

>	x:=t->1/t+ ln(2+t);y:=t->t+1/t;

>

>

>	Calculons le vecteur vitesse

>	Vt:=[D(x)(t),D(y)(t)];

>	Vt:=factor(Vt);

>	V:=unapply(Vt,t);

>

V(-1);

Cette courbe n'est donc régulière, le point de paramètre -1 est stationaire

>

>

>	Tangente aux points  A=M(-1)=(-1,-2), B=M(1)=(1+ln(3),0)  et C=M(2)=(1/2,5/2)

Les tangentes en B et C sont dirigées par les vecteurs

>	V(1);V(2);

D'où les équations des tangentes

>	XTB:=x(1)+t*op(1,V(1));YTB:=y(1)+t*op(2,V(1));

>	XTC:=x(2)+t*op(1,V(2));YTC:=y(2)+t*op(2,V(2));

>	EqTB:=[XTB,YTB,t=-infinity..infinity]:EqTC:=[XTC,YTC,t=-infinity..infinity]:

Tangente au point stationnaire A

Calculons la limite du taux d'accroissement en -1

>	Limit((y(t)-y(-1))/(x(t)-x(-1)),t=-1)=limit((y(t)-y(-1))/(x(t)-x(-1)),t=-1);

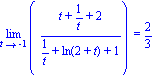
On en déduit donc une tangente horizontale au point de A paramètre -1

>	XTA:=x(-1)+t;YTA:=y(-1)+2*t/3;

>	EqTA:=[XTA,YTA,t=-infinity..infinity]:

Branches Infinies éventuelles en -2, 0 et +infinity

Etude en -2^+

>	Limit('x'(t),t=-2,right)=limit(x(t),t=-2,right),Limit('y'(t),t=-2,right)=limit(y(t),t=-2,right) ;

D'où une branche infinie lorsque t->-2^+, il s'agit d'une asymptote horizontale d'équation

>	XA1:=t;YA1:=-5/2;

>	EqA1:=[XA1,YA1,t=-infinity..infinity]:

Position Relative: pour cela on étudie le signe de y(tau)+5/2 pour tau proche de -2 (par valeurs supérieures)

>	assume(tau>-2):is(y(tau)+5/2>0);

#Vérifions le à l'aide de son expression algébrique:

>	factor(y(t)+5/2);

On a donc l'arc est "en  dessous" de cette asymptote.

Etude en 0^-

>	Limit('x'(t),t=0,left)=limit(x(t),t=0,left),Limit('y'(t),t=0,left)=limit(y(t),t=0,left) ;

D'où une branche infinie lorsque t->0^-,

Calculons la limite du taux y/x

>	Limit('y'(t)/'x'(t),t=0,left)=limit(y(t)/x(t),t=0,left);

La courbe admet donc une direction asymptotique la droite d'équation y=x.

Calculons alors la limite suivante

>	Limit('y'(t)-'x'(t),t=0,left)=limit(y(t)-x(t),t=0,left);

Donc la courbe admet une asymptote oblique d'équation y=x-ln(2)... d'où son équation paramétrique

>	XA2:=t;YA2:=t-ln(2);

>	EqA2:=[XA2,YA2,t=-infinity..infinity]:

>

Position Relative: pour cela on étudie le signe de y(tau)-x(tau)+ln(2) pour tau proche de -2 (par valeurs supérieures)

>	assume(tau<0 and tau>-1):is(combine(y(tau)-x(tau)+ln(2))>0);

Vérifions le à l'aide de son expression algébrique:

>	combine(y(t)-x(t)+ln(2));

or ceci est du signe opposé que la limite de  (y(t)-x(t)+ln(2))/t en O^-

>	Limit(('y'(t)-'x'(t)+ln(2))/t,t=0,left)=limit((y(t)-x(t)+ln(2))/t,t=0,left);

On a donc l'arc est "au  dessus" de cette asymptote.

>

Etude en 0^+

>	Limit('x'(t),t=0,right)=limit(x(t),t=0,right),Limit('y'(t),t=0,right)=limit(y(t),t=0,right) ;

D'où une branche infinie lorsque t->0^+,

Calculons la limite du taux y/x

>	Limit('y'(t)/'x'(t),t=0,right)=limit(y(t)/x(t),t=0,right);

La courbe admet donc une direction asymptotique la droite d'équation y=x.

Calculons alors la limite suivante

>	Limit('y'(t)-'x'(t),t=0,right)=limit(y(t)-x(t),t=0,right);

Donc la courbe admet une asymptote oblique d'équation y=x-ln(2)... d'où son équation paramétrique

>

Position Relative: pour cela on étudie le signe de y(tau)-x(tau)+ln(2) pour tau proche de -2 (par valeurs supérieures)

>	assume(tau>0 ):is(combine(y(tau)-x(tau)+ln(2))>0);

Vérifions le à l'aide de son expression algébrique:

>	combine(y(t)-x(t)+ln(2));

or ceci est du même que la limite de  (y(t)-x(t)+ln(2))/t en O^+

>	Limit(('y'(t)-'x'(t)+ln(2))/t,t=0,right)=limit((y(t)-x(t)+ln(2))/t,t=0,right);

On a donc l'arc est "au  dessus" de cette asymptote.

Etude en infinity

>	Limit('x'(t),t=infinity)=limit(x(t),t=infinity),Limit('y'(t),t=infinity)=limit(y(t),t=infinity) ;

>

D'où une branche infinie lorsque t->infinity,

Calculons la limite du taux y/x

>	Limit('y'(t)/'x'(t),t=infinity)=limit(y(t)/x(t),t=infinity);

La courbe admet donc une branche parabolique dans la direction de l'axe des ordonnées

Etude des variations de x et y

>	plot(x,-2..infinity);

>	plot(y,-2..infinity);

>	varx:=D(x)(t)/abs(D(x)(t)):

>	vary:=D(y)(t)/abs(D(y)(t))/2:

On trace en rouge le signe x' et en vert le signe de y'

>	plot([varx,vary],t=-2..5,discont=true,thickness=[3,3]);

>

Support de la courbe

>	total:=[x(t),y(t),t=-2..infinity]:

>	plot([total,EqTA,EqTB,EqTC,EqA1,EqA2],-5..5,-10..10,color=[blue,black,black,black,green,green],thickness=[3,1,1,1,2,2,2]);

Attention MAPLE semble ajouter à la courbe son asymptote!!!

>