| > | restart;with(linalg); |
Warning, the protected names norm and trace have been redefined and unprotected
![]()
![]()
![]()
![]()
| > |
| > |
| > | Exercice 24 |
| > |
question a)
| > | A:=matrix([[1,1,0],[0,4,1],[4,0,4]]); |
![A := matrix([[1, 1, 0], [0, 4, 1], [4, 0, 4]])](images/Exo24_5.gif)
| > | P:=matrix([[1,1,-1],[4,1,0],[4,-2,1]]); |
![P := matrix([[1, 1, -1], [4, 1, 0], [4, -2, 1]])](images/Exo24_6.gif)
| > | Grang(P); |
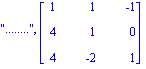
![L[2],](images/Exo24_8.gif)
![L[3],](images/Exo24_9.gif)
![L[2],](images/Exo24_10.gif)
![L[3],](images/Exo24_11.gif)
![L[3],](images/Exo24_12.gif)
Donc rang(P)=3, P est donc inversible, calculons son inverse.
Méthode 1: A l'aide du système associé
| > | Gsyst_cramer(P,[x,y,z],[a,b,c]); |
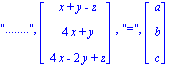
![L[2],](images/Exo24_14.gif)
![L[3],](images/Exo24_15.gif)
![L[2],](images/Exo24_16.gif)
![L[3],](images/Exo24_17.gif)
![L[3],](images/Exo24_18.gif)
![L[1],](images/Exo24_19.gif)
![L[2],](images/Exo24_20.gif)
![L[1],](images/Exo24_21.gif)
Méthode 2: A l'aide des opérations élémentaires issues du pivot de Gauss appliqué à la matrice Identité
| > | Ginverse(P); |
![matrix([[1, 1, -1], [4, 1, 0], [4, -2, 1]]),](images/Exo24_22.gif)
![matrix([[1, 1, -1], [0, -3, 4], [4, -2, 1]]), L[2],](images/Exo24_23.gif)
![matrix([[1, 1, -1], [0, -3, 4], [0, -6, 5]]), L[3],](images/Exo24_24.gif)
![matrix([[1, 1, -1], [0, 1, (-4)/3], [0, -6, 5]]), L[2],](images/Exo24_25.gif)
![matrix([[1, 1, -1], [0, 1, (-4)/3], [0, 0, -3]]), L[3],](images/Exo24_26.gif)
![matrix([[1, 1, -1], [0, 1, (-4)/3], [0, 0, 1]]), L[3],](images/Exo24_27.gif)
![matrix([[1, 1, 0], [0, 1, (-4)/3], [0, 0, 1]]), L[1],](images/Exo24_28.gif)
![matrix([[1, 1, 0], [0, 1, 0], [0, 0, 1]]), L[2],](images/Exo24_29.gif)
![matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]]), L[1],](images/Exo24_30.gif)
| > | inv_P:=inverse(P); |
![inv_P := matrix([[1/9, 1/9, 1/9], [(-4)/9, 5/9, (-4)/9], [(-4)/3, 2/3, (-1)/3]])](images/Exo24_31.gif)
question b) et c)
| > |
| > | inv_PAP=evalm(inv_P&*A&*P); |
![inv_PAP = matrix([[5, 0, 0], [0, 2, 1], [0, 0, 2]])](images/Exo24_32.gif)
C'est en fait la matrice B associée à l'application canoniquement associée à A, relativement à la base (e1, e2, e3) formée des colonnes de P
| > | B:=evalm(inv_P&*A&*P); |
![B := matrix([[5, 0, 0], [0, 2, 1], [0, 0, 2]])](images/Exo24_33.gif)
| > |
| > | question d) |
| > | J:=matrix([[5,0,0],[0,2,0],[0,0,2]]); |
![J := matrix([[5, 0, 0], [0, 2, 0], [0, 0, 2]])](images/Exo24_34.gif)
| > | K:=matrix([[0,0,0],[0,0,1],[0,0,0]]); |
![K := matrix([[0, 0, 0], [0, 0, 1], [0, 0, 0]])](images/Exo24_35.gif)
| > | JK:=evalm(J&*K); |
![JK := matrix([[0, 0, 0], [0, 0, 2], [0, 0, 0]])](images/Exo24_36.gif)
| > | KJ:=evalm(K&*J); |
![KJ := matrix([[0, 0, 0], [0, 0, 2], [0, 0, 0]])](images/Exo24_37.gif)
| > | evalm(K^2); |
![matrix([[0, 0, 0], [0, 0, 0], [0, 0, 0]])](images/Exo24_38.gif)
et donc pour tout n>1 K^n=0
| > | evalm(J^2);evalm(J^3); |
![matrix([[25, 0, 0], [0, 4, 0], [0, 0, 4]])](images/Exo24_39.gif)
![matrix([[125, 0, 0], [0, 8, 0], [0, 0, 8]])](images/Exo24_40.gif)
et par récurrence pour tout entier n, J^n=diag(5^n,2^n,2^n)
| > |
| > |
Ainsi K et J commutent on peut appliquer la formule de Newton
| > | B^n=(K+J)^n,"=",Sum(Cn^p*K^p*J^(n-p),p=0..n),"=",J^n+n*K*J^(n-1); |
![]()
| > | Bn:=evalm(diagonale([[5^n,2^n,2^n]])+K&*diagonale([[n*5^(n-1),n*2^(n-1),n*2^(n-1)]])): |
| > | B^n=evalm(Bn); |
![B^n = matrix([[5^n, 0, 0], [0, 2^n, n*2^(n-1)], [0, 0, 2^n]])](images/Exo24_42.gif)
Or ('P'*'B'*inv_P)^n='P'*'B'^n*inv_P; d'où
![]()
| > | An:=evalm(P&*B(n)&*inv_P):A^n=evalm(An); |
![A^n = matrix([[1/9*5^n+8/9*2^n-4/3*n*2^(n-1), 1/9*5^n-1/9*2^n+2/3*n*2^(n-1), 1/9*5^n-1/9*2^n-1/3*n*2^(n-1)], [4/9*5^n-4/9*2^n-4/3*n*2^(n-1), 4/9*5^n+5/9*2^n+2/3*n*2^(n-1), 4/9*5^n-4/9*2^n-1/3*n*2^(n-1...](images/Exo24_44.gif)
| > |