| > | restart;with(linalg); |
Warning, the protected names norm and trace have been redefined and unprotected
![]()
![]()
![]()
![]()
| > | Exercice 2 |
question a)
| > | j:=exp(I*2*Pi/3):j:='j':m:='m':x:='x':y:='y':z:='z': |
| > | S:=matrix(3,4,[[x,j*y,z,3],[j*x,j^2*y,z,m],[j^2*x,y,z,2*m]]); |
![S := matrix([[x, j*y, z, 3], [j*x, j^2*y, z, m], [j^2*x, y, z, 2*m]])](images/exo2_5.gif)
| > | S:=Transvect_ligne(2,-j,1,S); |
![S := matrix([[x, j*y, z, 3], [0, 0, z-j*z, m-3*j], [j^2*x, y, z, 2*m]])](images/exo2_6.gif)
| > | S:=Transvect_ligne(3,-j^2,1,S); |
![S := matrix([[x, j*y, z, 3], [0, 0, z-j*z, m-3*j], [0, y-j^3*y, z-j^2*z, 2*m-3*j^2]])](images/exo2_7.gif)
| > | S:=Permut_colonne(2,3,S); |
![S := matrix([[x, z, j*y, 3], [0, z-j*z, 0, m-3*j], [0, z-j^2*z, y-j^3*y, 2*m-3*j^2]])](images/exo2_8.gif)
| > | evalm(S); |
![matrix([[x, z, j*y, 3], [0, z-j*z, 0, m-3*j], [0, z-j^2*z, y-j^3*y, 2*m-3*j^2]])](images/exo2_9.gif)
| > | S:=Dilat_ligne(1/(1-j),2,S); |
![S := matrix([[x, z, j*y, 3], [0, z, 0, (-m+3*j)/(-1+j)], [0, z-j^2*z, y-j^3*y, 2*m-3*j^2]])](images/exo2_10.gif)
| > | S:=Transvect_ligne(3,j^2-1,2,S); |
![S := matrix([[x, z, j*y, 3], [0, z, 0, (-m+3*j)/(-1+j)], [0, 0, y-j^3*y, 3*j-m*j+m]])](images/exo2_11.gif)
| > | S[3,2]:=0:S[3,3]:=0:S[2,2]:=z: |
| > | evalm(S); |
![matrix([[x, z, j*y, 3], [0, z, 0, (-m+3*j)/(-1+j)], [0, 0, 0, 3*j-m*j+m]])](images/exo2_12.gif)
| > |
Equation de compatibilité:
| > | Eq_comp:=S[3,4]=0; |
![]()
| > | m:=solve(Eq_comp,m); |
![]()
y est un paramètre libre et
| > | z:=simplify(S[2,4]);
|
![]()
| > | x:=3-z-j*y; |
![]()
| > |
| > |
question b)
| > | l:='l':lambda:='lambda':l:=lambda:a:='a':x:='x':y:='y':z:='z': |
| > | S0:=matrix(4,5,[[l*x,y,z,t,a^3],[x,l*y,z,t,a^2],[x,y,l*z,t,a],[x,y,z,l*t,1]]); |
![S0 := matrix([[lambda*x, y, z, t, a^3], [x, lambda*y, z, t, a^2], [x, y, lambda*z, t, a], [x, y, z, lambda*t, 1]])](images/exo2_17.gif)
| > | A0:=matrix(4,4,[[l,1,1,1],[1,l,1,1],[1,1,l,1],[1,1,1,l]]); |
![A0 := matrix([[lambda, 1, 1, 1], [1, lambda, 1, 1], [1, 1, lambda, 1], [1, 1, 1, lambda]])](images/exo2_18.gif)
| > |
1er Cas
| > | On suppose l, "différent de ", 0,1,-1,-2,-3; |
![]()
| > | S:=evalm(S0); |
| > | S:=Dilat_ligne(1/l,1,S); |
![S := matrix([[x, y/lambda, z/lambda, t/lambda, a^3/lambda], [x, lambda*y, z, t, a^2], [x, y, lambda*z, t, a], [x, y, z, lambda*t, 1]])](images/exo2_20.gif)
| > | S:=Transvect_ligne(2,-1,1,S):S:=Transvect_ligne(3,-1,1,S):S:=Transvect_ligne(4,-1,1,S); |
![S := matrix([[x, y/lambda, z/lambda, t/lambda, a^3/lambda], [0, y*(lambda^2-1)/lambda, z*(lambda-1)/lambda, t*(lambda-1)/lambda, -a^2*(-lambda+a)/lambda], [0, y*(lambda-1)/lambda, z*(lambda^2-1)/lambd...](images/exo2_21.gif)
| > | S:=Dilat_ligne(l/(l^2-1),2,S); |
![S := matrix([[x, y/lambda, z/lambda, t/lambda, a^3/lambda], [0, y, z/(lambda+1), t/(lambda+1), -a^2*(-lambda+a)/(lambda^2-1)], [0, y*(lambda-1)/lambda, z*(lambda^2-1)/lambda, t*(lambda-1)/lambda, -a*(...](images/exo2_22.gif)
| > |
| > | S:=Transvect_ligne(3,1/l-1,2,S):S:=Transvect_ligne(4,1/l-1,2,S); |
![S := matrix([[x, y/lambda, z/lambda, t/lambda, a^3/lambda], [0, y, z/(lambda+1), t/(lambda+1), -a^2*(-lambda+a)/(lambda^2-1)], [0, 0, z*(lambda^2+lambda-2)/(lambda+1), t*(lambda-1)/(lambda+1), -(-lamb...](images/exo2_23.gif)
| > | S:=Dilat_ligne(z/S[3,3],3,S); |
![S := matrix([[x, y/lambda, z/lambda, t/lambda, a^3/lambda], [0, y, z/(lambda+1), t/(lambda+1), -a^2*(-lambda+a)/(lambda^2-1)], [0, 0, z, t/(lambda+2), -(-lambda+a^2+a-1)*a/(lambda^2+lambda-2)], [0, 0,...](images/exo2_24.gif)
| > | S:=Transvect_ligne(4,-(l-1)/(l+1),3,S); |
![S := matrix([[x, y/lambda, z/lambda, t/lambda, a^3/lambda], [0, y, z/(lambda+1), t/(lambda+1), -a^2*(-lambda+a)/(lambda^2-1)], [0, 0, z, t/(lambda+2), -(-lambda+a^2+a-1)*a/(lambda^2+lambda-2)], [0, 0,...](images/exo2_25.gif)
| > | S:=Dilat_ligne(t/S[4,4],4,S); |
![S := matrix([[x, y/lambda, z/lambda, t/lambda, a^3/lambda], [0, y, z/(lambda+1), t/(lambda+1), -a^2*(-lambda+a)/(lambda^2-1)], [0, 0, z, t/(lambda+2), -(-lambda+a^2+a-1)*a/(lambda^2+lambda-2)], [0, 0,...](images/exo2_26.gif)
| > | S:=Transvect_ligne(3,-S[3,4]/t,4,S):S:=Transvect_ligne(2,-S[2,4]/t,4,S):S:=Transvect_ligne(1,-S[1,4]/t,4,S); |
![S := matrix([[x, y/lambda, z/lambda, 0, (a^3*lambda^2+2*a^3*lambda-2*a^3-lambda+a-2+a^2)/(lambda*(lambda^2+2*lambda-3))], [0, y, z/(lambda+1), 0, -(-a^2*lambda^2+a^3*lambda-3*a^2*lambda+lambda+2*a^3+2...](images/exo2_27.gif)
| > | S:=Transvect_ligne(2,-S[2,3]/z,3,S):S:=Transvect_ligne(1,-S[1,3]/z,3,S); |
![S := matrix([[x, y/lambda, 0, 0, (a^3*lambda^2+2*a^3*lambda-a^3-lambda-a-1+2*a^2-a*lambda)/(lambda*(lambda^2+2*lambda-3))], [0, y, 0, 0, -(-a^2*lambda+a^3+1+a-2*a^2)/(lambda^2+2*lambda-3)], [0, 0, z, ...](images/exo2_28.gif)
| > | S:=Transvect_ligne(1,-S[1,2]/y,2,S); |
![S := matrix([[x, 0, 0, 0, (a^3*lambda+2*a^3-1-a-a^2)/(lambda^2+2*lambda-3)], [0, y, 0, 0, -(-a^2*lambda+a^3+1+a-2*a^2)/(lambda^2+2*lambda-3)], [0, 0, z, 0, -(-a*lambda+a^2+1-2*a+a^3)/(lambda^2+2*lambd...](images/exo2_29.gif)
Voilà la solution du système de CRAMER
| > |
2eme Cas
| > | On suppose lambda=0; |
![]()
| > | A:=subs(lambda=0,evalm(A0));
|
![A := matrix([[0, 1, 1, 1], [1, 0, 1, 1], [1, 1, 0, 1], [1, 1, 1, 0]])](images/exo2_31.gif)
| > | Gsyst_cramer(A,[x,y,z,t],[a^3,a^2,a,1]); |
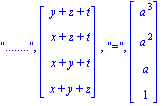
![L[2],](images/exo2_33.gif) ", L[1], matrix([[x+z+t], [y+z+t], [x+y+t], [x+y+z]]), "=", matrix([[a^2], [a^3], [a], [1]])" align="center">
", L[1], matrix([[x+z+t], [y+z+t], [x+y+t], [x+y+z]]), "=", matrix([[a^2], [a^3], [a], [1]])" align="center">
![L[3],](images/exo2_34.gif)
![L[4],](images/exo2_35.gif)
![L[3],](images/exo2_36.gif)
![L[4],](images/exo2_37.gif)
![L[3],](images/exo2_38.gif)
![L[4],](images/exo2_39.gif)
![L[4],](images/exo2_40.gif)
![L[1],](images/exo2_41.gif)
![L[2],](images/exo2_42.gif)
![L[3],](images/exo2_43.gif)
![L[1],](images/exo2_44.gif)
![L[2],](images/exo2_45.gif)
| > |
3eme Cas
| > | On suppose lambda=1; |
![]()
| > | A:=subs(lambda=1,evalm(A0));
|
![A := matrix([[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]])](images/exo2_47.gif)
| > | Gsyst(A,[x,y,z,t],[a^3,a^2,a,1]): |

![L[2],](images/exo2_49.gif)
![L[3],](images/exo2_50.gif)
![L[4],](images/exo2_51.gif)
![C[2],](images/exo2_52.gif) ", C[3], matrix([[x, z, y, t], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]), "=", matrix([[a^3], [a^2-a^3], [a-a^3], [1-a^3]])" align="center">
", C[3], matrix([[x, z, y, t], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]), "=", matrix([[a^3], [a^2-a^3], [a-a^3], [1-a^3]])" align="center">
![C[2],](images/exo2_53.gif) ", C[4], matrix([[x, t, y, z], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]), "=", matrix([[a^3], [a^2-a^3], [a-a^3], [1-a^3]])" align="center">
", C[4], matrix([[x, t, y, z], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]), "=", matrix([[a^3], [a^2-a^3], [a-a^3], [1-a^3]])" align="center">
![C[3],](images/exo2_54.gif) ", C[4], matrix([[x, t, z, y], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]), "=", matrix([[a^3], [a^2-a^3], [a-a^3], [1-a^3]])" align="center">
", C[4], matrix([[x, t, z, y], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]), "=", matrix([[a^3], [a^2-a^3], [a-a^3], [1-a^3]])" align="center">
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | D'où nécessairement a=1; |
![]()
| > | Et on trouve l'hyperplan x+y+z+t=1; |
![]()
| > |
4eme Cas
| > | On suppose lambda=-1; |
![]()
| > | A:=subs(lambda=-1,evalm(A0));
|
![A := matrix([[-1, 1, 1, 1], [1, -1, 1, 1], [1, 1, -1, 1], [1, 1, 1, -1]])](images/exo2_65.gif)
| > | Gsyst_cramer(A,[x,y,z,t],[a^3,a^2,a,1]): |

![L[1],](images/exo2_67.gif)
![L[2],](images/exo2_68.gif)
![L[3],](images/exo2_69.gif)
![L[4],](images/exo2_70.gif)
![L[3],](images/exo2_71.gif) ", L[2], matrix([[x-y-z-t], [2*y+2*t], [2*z+2*t], [2*y+2*z]]), "=", matrix([[-a^3], [a+a^3], [a^2+a^3], [1+a^3]])" align="center">
", L[2], matrix([[x-y-z-t], [2*y+2*t], [2*z+2*t], [2*y+2*z]]), "=", matrix([[-a^3], [a+a^3], [a^2+a^3], [1+a^3]])" align="center">
![L[2],](images/exo2_72.gif)
![L[4],](images/exo2_73.gif)
![L[3],](images/exo2_74.gif)
![L[4],](images/exo2_75.gif)
![L[4],](images/exo2_76.gif)
![L[1],](images/exo2_77.gif)
![L[2],](images/exo2_78.gif)
![L[3],](images/exo2_79.gif)
![L[1],](images/exo2_80.gif)
![L[1],](images/exo2_81.gif)
| > |
| > |
5eme Cas
| > | On suppose lambda=-2; |
![]()
| > | A:=subs(lambda=-2,evalm(A0));
|
![A := matrix([[-2, 1, 1, 1], [1, -2, 1, 1], [1, 1, -2, 1], [1, 1, 1, -2]])](images/exo2_83.gif)
| > | Gsyst_cramer(A,[x,y,z,t],[a^3,a^2,a,1]): |
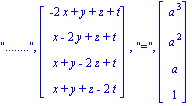
![L[1],](images/exo2_85.gif)
![L[2],](images/exo2_86.gif)
![L[3],](images/exo2_87.gif)
![L[4],](images/exo2_88.gif)
![L[2],](images/exo2_89.gif)
![L[3],](images/exo2_90.gif)
![L[4],](images/exo2_91.gif)
![L[4],](images/exo2_92.gif) ", L[3], matrix([[x-1/2*y-1/2*z-1/2*t], [y-z-t], [3*z], [3*t]]), "=", matrix([[-1/2*a^3], [-2/3*a^2-1/3*a^3], [1+a^3+a^2], [a+a^3+a^2]])" align="center">
", L[3], matrix([[x-1/2*y-1/2*z-1/2*t], [y-z-t], [3*z], [3*t]]), "=", matrix([[-1/2*a^3], [-2/3*a^2-1/3*a^3], [1+a^3+a^2], [a+a^3+a^2]])" align="center">
![L[3],](images/exo2_93.gif)
![L[4],](images/exo2_94.gif)
![L[1],](images/exo2_95.gif)
![L[2],](images/exo2_96.gif)
![L[1],](images/exo2_97.gif)
![L[2],](images/exo2_98.gif)
![L[1],](images/exo2_99.gif)
| > |
6eme Cas
| > | On suppose lambda=-3; |
![]()
| > | A:=subs(lambda=-3,evalm(A0));
|
![A := matrix([[-3, 1, 1, 1], [1, -3, 1, 1], [1, 1, -3, 1], [1, 1, 1, -3]])](images/exo2_101.gif)
| > | Gsyst(A,[x,y,z,t],[a^3,a^2,a,1]): |
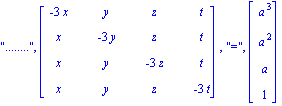
![L[1],](images/exo2_103.gif)
![L[2],](images/exo2_104.gif)
![L[3],](images/exo2_105.gif)
![L[4],](images/exo2_106.gif)
![L[2],](images/exo2_107.gif)
![L[3],](images/exo2_108.gif)
![L[4],](images/exo2_109.gif)
![L[3],](images/exo2_110.gif)
![L[4],](images/exo2_111.gif)
![]()
![]()
![]()
![]()
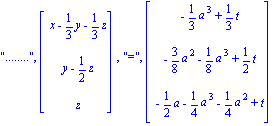
![L[1],](images/exo2_117.gif)
![L[2],](images/exo2_118.gif)
![L[1],](images/exo2_119.gif)
| > | last:=matrix([[-1/2*a^3+t-1/4*a-1/4*a^2], [-1/2*a^2-1/4*a^3+t-1/4*a], [-1/2*a-1/4*a^3-1/4*a^2+t], [t]]); |
![last := matrix([[-1/2*a^3+t-1/4*a-1/4*a^2], [-1/2*a^2-1/4*a^3+t-1/4*a], [-1/2*a-1/4*a^3-1/4*a^2+t], [t]])](images/exo2_120.gif)
Equation de compatibilité:
| > | Eq_comp:=1+a+a^2+a^3=0; |
![]()
| > | a_possible:=solve(Eq_comp,a); |
![]()
D'où trois espaces affines possibles:
| > | matrix([[x], [y], [z], [t]])=subs(a=a_possible[1],evalm(last));
|
![matrix([[x], [y], [z], [t]]) = matrix([[1/2+t], [t], [1/2+t], [t]])](images/exo2_123.gif)
| > | matrix([[x], [y], [z], [t]])=subs(a=a_possible[2],evalm(last)); |
![matrix([[x], [y], [z], [t]]) = matrix([[(1/4+1/4*I)+t], [1/2+t], [(1/4-1/4*I)+t], [t]])](images/exo2_124.gif)
| > | matrix([[x], [y], [z], [t]])=subs(a=a_possible[3],evalm(last)); |
![matrix([[x], [y], [z], [t]]) = matrix([[(1/4-1/4*I)+t], [1/2+t], [(1/4+1/4*I)+t], [t]])](images/exo2_125.gif)
Seule la solution particulière change la direction vectorielle est dirigé par le vecteur
| > | u:=[1,1,1,1]; |
![]()
Autre Méthode:
1er Cas
| > | On suppose l, "différent de ", 1,-3; |
![]()
| > | S:=evalm(S0); |
![S := matrix([[lambda*x, y, z, t, a^3], [x, lambda*y, z, t, a^2], [x, y, lambda*z, t, a], [x, y, z, lambda*t, 1]])](images/exo2_128.gif)
| > | S:=Permut_ligne(1,2,S); |
![S := matrix([[x, lambda*y, z, t, a^2], [lambda*x, y, z, t, a^3], [x, y, lambda*z, t, a], [x, y, z, lambda*t, 1]])](images/exo2_129.gif)
| > | S:=Transvect_ligne(2,-l,1,S):S:=Transvect_ligne(3,-1,1,S):S:=Transvect_ligne(4,-1,1,S); |
![S := matrix([[x, lambda*y, z, t, a^2], [0, y-lambda^2*y, z-lambda*z, t-lambda*t, a^3-lambda*a^2], [0, y-lambda*y, lambda*z-z, 0, a-a^2], [0, y-lambda*y, 0, lambda*t-t, 1-a^2]])](images/exo2_130.gif)
| > | S:=Permut_ligne(2,3,S); |
![S := matrix([[x, lambda*y, z, t, a^2], [0, y-lambda*y, lambda*z-z, 0, a-a^2], [0, y-lambda^2*y, z-lambda*z, t-lambda*t, a^3-lambda*a^2], [0, y-lambda*y, 0, lambda*t-t, 1-a^2]])](images/exo2_131.gif)
| > | S:=Dilat_ligne(1/(1-l),2,S); |
![S := matrix([[x, lambda*y, z, t, a^2], [0, y, -z, 0, a*(-1+a)/(-1+lambda)], [0, y-lambda^2*y, z-lambda*z, t-lambda*t, a^3-lambda*a^2], [0, y-lambda*y, 0, lambda*t-t, 1-a^2]])](images/exo2_132.gif)
| > | S:=Transvect_ligne(3,l^2-1,2,S):S:=Transvect_ligne(4,l-1,2,S); |
![S := matrix([[x, lambda*y, z, t, a^2], [0, y, -z, 0, a*(-1+a)/(-1+lambda)], [0, 0, 2*z-lambda*z-z*lambda^2, t-lambda*t, (-lambda+a+a^2-1)*a], [0, 0, -(-1+lambda)*z, lambda*t-t, 1-a]])](images/exo2_133.gif)
| > | S:=Permut_ligne(3,4,S); |
![S := matrix([[x, lambda*y, z, t, a^2], [0, y, -z, 0, a*(-1+a)/(-1+lambda)], [0, 0, -(-1+lambda)*z, lambda*t-t, 1-a], [0, 0, 2*z-lambda*z-z*lambda^2, t-lambda*t, (-lambda+a+a^2-1)*a]])](images/exo2_134.gif)
| > | S:=Dilat_ligne(1/(1-l),3,S); |
![S := matrix([[x, lambda*y, z, t, a^2], [0, y, -z, 0, a*(-1+a)/(-1+lambda)], [0, 0, z, -t, (-1+a)/(-1+lambda)], [0, 0, 2*z-lambda*z-z*lambda^2, t-lambda*t, (-lambda+a+a^2-1)*a]])](images/exo2_135.gif)
| > | S:=Transvect_ligne(4,-(2-l-l^2),3,S); |
![S := matrix([[x, lambda*y, z, t, a^2], [0, y, -z, 0, a*(-1+a)/(-1+lambda)], [0, 0, z, -t, (-1+a)/(-1+lambda)], [0, 0, 0, 3*t-2*lambda*t-t*lambda^2, -lambda+a^2+a^3-2+a]])](images/exo2_136.gif)
| > | S:=Dilat_ligne(1/(3-2*l-l^2),4,S); |
![S := matrix([[x, lambda*y, z, t, a^2], [0, y, -z, 0, a*(-1+a)/(-1+lambda)], [0, 0, z, -t, (-1+a)/(-1+lambda)], [0, 0, 0, t, -(-lambda+a^2+a^3-2+a)/(-3+2*lambda+lambda^2)]])](images/exo2_137.gif)
| > | S:=Transvect_ligne(3,1,4,S):S:=Transvect_ligne(1,-1,4,S); |
![S := matrix([[x, lambda*y, z, 0, (-2*a^2+2*lambda*a^2+a^2*lambda^2-lambda+a^3-2+a)/(-3+2*lambda+lambda^2)], [0, y, -z, 0, a*(-1+a)/(-1+lambda)], [0, 0, z, 0, -(-lambda*a-2*a+1+a^3+a^2)/(-3+2*lambda+la...](images/exo2_138.gif)
| > | S:=Transvect_ligne(2,1,3,S):S:=Transvect_ligne(1,-1,3,S); |
![S := matrix([[x, lambda*y, 0, 0, (-a^2+2*lambda*a^2+a^2*lambda^2-lambda+2*a^3-1-a-lambda*a)/(-3+2*lambda+lambda^2)], [0, y, 0, 0, -(-lambda*a^2+a^3+a+1-2*a^2)/(-3+2*lambda+lambda^2)], [0, 0, z, 0, -(-...](images/exo2_139.gif)
| > | S:=Transvect_ligne(1,-l,2,S); |
![S := matrix([[x, 0, 0, 0, (-a^2+2*a^3-1-a+lambda*a^3)/(-3+2*lambda+lambda^2)], [0, y, 0, 0, -(-lambda*a^2+a^3+a+1-2*a^2)/(-3+2*lambda+lambda^2)], [0, 0, z, 0, -(-lambda*a-2*a+1+a^3+a^2)/(-3+2*lambda+l...](images/exo2_140.gif)
Voilà la solution du système de CRAMER dans le cas lambda différent de 1 et -3
| > |