| > | restart;with(linalg); |
Warning, the protected names norm and trace have been redefined and unprotected
![]()
![]()
![]()
![]()
| > |
| > | Exercice 3 |
| > | question a) |
| > | A:=matrix(5,5,[[2,1,-1,0,1],[1,-10,0,-1,-2],[1,2,-1,1,2],[2,-2,1,-1,1],[2,2,1,0,2]]); |
![A := matrix([[2, 1, -1, 0, 1], [1, -10, 0, -1, -2], [1, 2, -1, 1, 2], [2, -2, 1, -1, 1], [2, 2, 1, 0, 2]])](images/exo3_5.gif)
| > | B:=matrix(4,4,[[2,1,-1,0],[1,-10,0,-1],[1,2,-1,1],[2,-2,1,-1]]); |
![B := matrix([[2, 1, -1, 0], [1, -10, 0, -1], [1, 2, -1, 1], [2, -2, 1, -1]])](images/exo3_6.gif)
Calculons les rangs de ces matrices
| > | Grang(A); |

![L[1],](images/exo3_8.gif)
![L[2],](images/exo3_9.gif)
![L[3],](images/exo3_10.gif)
![L[4],](images/exo3_11.gif)
![L[5],](images/exo3_12.gif)
![L[2],](images/exo3_13.gif)
![L[3],](images/exo3_14.gif)
![L[4],](images/exo3_15.gif)
![L[5],](images/exo3_16.gif)
![L[3],](images/exo3_17.gif)
![L[4],](images/exo3_18.gif)
![L[5],](images/exo3_19.gif)
![L[4],](images/exo3_20.gif)
![L[5],](images/exo3_21.gif)
![L[5],](images/exo3_22.gif)
donc rang(A)=5, A est donc inversible
| > | Grang(B); |
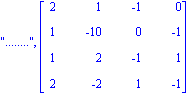
![L[1],](images/exo3_24.gif)
![L[2],](images/exo3_25.gif)
![L[3],](images/exo3_26.gif)
![L[4],](images/exo3_27.gif)
![L[2],](images/exo3_28.gif)
![L[3],](images/exo3_29.gif)
![L[4],](images/exo3_30.gif)
![L[3],](images/exo3_31.gif)
![L[4],](images/exo3_32.gif)
![L[4],](images/exo3_33.gif)
| > | donc rang(B)=4, B est donc inversible |
| > | question b) |
Calculons les inverses:
Methode 1 pour A, on applique à la matrice identité les opérations sur les lignes issues du pivot de Gauss relatif à A
| > | Ginverse(A); |
![matrix([[2, 1, -1, 0, 1], [1, -10, 0, -1, -2], [1, 2, -1, 1, 2], [2, -2, 1, -1, 1], [2, 2, 1, 0, 2]]),](images/exo3_34.gif)
![matrix([[1, 1/2, (-1)/2, 0, 1/2], [1, -10, 0, -1, -2], [1, 2, -1, 1, 2], [2, -2, 1, -1, 1], [2, 2, 1, 0, 2]]), L[1],](images/exo3_35.gif)
![matrix([[1, 1/2, (-1)/2, 0, 1/2], [0, (-21)/2, 1/2, -1, (-5)/2], [1, 2, -1, 1, 2], [2, -2, 1, -1, 1], [2, 2, 1, 0, 2]]), L[2],](images/exo3_36.gif)
![matrix([[1, 1/2, (-1)/2, 0, 1/2], [0, (-21)/2, 1/2, -1, (-5)/2], [0, 3/2, (-1)/2, 1, 3/2], [2, -2, 1, -1, 1], [2, 2, 1, 0, 2]]), L[3],](images/exo3_37.gif)
![matrix([[1, 1/2, (-1)/2, 0, 1/2], [0, (-21)/2, 1/2, -1, (-5)/2], [0, 3/2, (-1)/2, 1, 3/2], [0, -3, 2, -1, 0], [2, 2, 1, 0, 2]]), L[4],](images/exo3_38.gif)
![matrix([[1, 1/2, (-1)/2, 0, 1/2], [0, (-21)/2, 1/2, -1, (-5)/2], [0, 3/2, (-1)/2, 1, 3/2], [0, -3, 2, -1, 0], [0, 1, 2, 0, 1]]), L[5],](images/exo3_39.gif)
![matrix([[1, 1/2, (-1)/2, 0, 1/2], [0, 1, (-1)/21, 2/21, 5/21], [0, 3/2, (-1)/2, 1, 3/2], [0, -3, 2, -1, 0], [0, 1, 2, 0, 1]]), L[2],](images/exo3_40.gif)
![matrix([[1, 1/2, (-1)/2, 0, 1/2], [0, 1, (-1)/21, 2/21, 5/21], [0, 0, (-3)/7, 6/7, 8/7], [0, -3, 2, -1, 0], [0, 1, 2, 0, 1]]), L[3],](images/exo3_41.gif)
![matrix([[1, 1/2, (-1)/2, 0, 1/2], [0, 1, (-1)/21, 2/21, 5/21], [0, 0, (-3)/7, 6/7, 8/7], [0, 0, 13/7, (-5)/7, 5/7], [0, 1, 2, 0, 1]]), L[4],](images/exo3_42.gif)
![matrix([[1, 1/2, (-1)/2, 0, 1/2], [0, 1, (-1)/21, 2/21, 5/21], [0, 0, (-3)/7, 6/7, 8/7], [0, 0, 13/7, (-5)/7, 5/7], [0, 0, 43/21, (-2)/21, 16/21]]), L[5],](images/exo3_43.gif)
![matrix([[1, 1/2, (-1)/2, 0, 1/2], [0, 1, (-1)/21, 2/21, 5/21], [0, 0, 1, -2, (-8)/3], [0, 0, 13/7, (-5)/7, 5/7], [0, 0, 43/21, (-2)/21, 16/21]]), L[3],](images/exo3_44.gif)
![matrix([[1, 1/2, (-1)/2, 0, 1/2], [0, 1, (-1)/21, 2/21, 5/21], [0, 0, 1, -2, (-8)/3], [0, 0, 0, 3, 17/3], [0, 0, 43/21, (-2)/21, 16/21]]), L[4],](images/exo3_45.gif)
![matrix([[1, 1/2, (-1)/2, 0, 1/2], [0, 1, (-1)/21, 2/21, 5/21], [0, 0, 1, -2, (-8)/3], [0, 0, 0, 3, 17/3], [0, 0, 0, 4, 56/9]]), L[5],](images/exo3_46.gif)
![matrix([[1, 1/2, (-1)/2, 0, 1/2], [0, 1, (-1)/21, 2/21, 5/21], [0, 0, 1, -2, (-8)/3], [0, 0, 0, 1, 17/9], [0, 0, 0, 4, 56/9]]), L[4],](images/exo3_47.gif)
![matrix([[1, 1/2, (-1)/2, 0, 1/2], [0, 1, (-1)/21, 2/21, 5/21], [0, 0, 1, -2, (-8)/3], [0, 0, 0, 1, 17/9], [0, 0, 0, 0, (-4)/3]]), L[5],](images/exo3_48.gif)
![matrix([[1, 1/2, (-1)/2, 0, 1/2], [0, 1, (-1)/21, 2/21, 5/21], [0, 0, 1, -2, (-8)/3], [0, 0, 0, 1, 17/9], [0, 0, 0, 0, 1]]), L[5],](images/exo3_49.gif)
![matrix([[1, 1/2, (-1)/2, 0, 0], [0, 1, (-1)/21, 2/21, 5/21], [0, 0, 1, -2, (-8)/3], [0, 0, 0, 1, 17/9], [0, 0, 0, 0, 1]]), L[1],](images/exo3_50.gif)
![matrix([[1, 1/2, (-1)/2, 0, 0], [0, 1, (-1)/21, 2/21, 0], [0, 0, 1, -2, (-8)/3], [0, 0, 0, 1, 17/9], [0, 0, 0, 0, 1]]), L[2],](images/exo3_51.gif)
![matrix([[1, 1/2, (-1)/2, 0, 0], [0, 1, (-1)/21, 2/21, 0], [0, 0, 1, -2, 0], [0, 0, 0, 1, 17/9], [0, 0, 0, 0, 1]]), L[3],](images/exo3_52.gif)
![matrix([[1, 1/2, (-1)/2, 0, 0], [0, 1, (-1)/21, 2/21, 0], [0, 0, 1, -2, 0], [0, 0, 0, 1, 0], [0, 0, 0, 0, 1]]), L[4],](images/exo3_53.gif)
![matrix([[1, 1/2, (-1)/2, 0, 0], [0, 1, (-1)/21, 0, 0], [0, 0, 1, -2, 0], [0, 0, 0, 1, 0], [0, 0, 0, 0, 1]]), L[2],](images/exo3_54.gif)
![matrix([[1, 1/2, (-1)/2, 0, 0], [0, 1, (-1)/21, 0, 0], [0, 0, 1, 0, 0], [0, 0, 0, 1, 0], [0, 0, 0, 0, 1]]), L[3],](images/exo3_55.gif)
![matrix([[1, 1/2, 0, 0, 0], [0, 1, (-1)/21, 0, 0], [0, 0, 1, 0, 0], [0, 0, 0, 1, 0], [0, 0, 0, 0, 1]]), L[1],](images/exo3_56.gif)
![matrix([[1, 1/2, 0, 0, 0], [0, 1, 0, 0, 0], [0, 0, 1, 0, 0], [0, 0, 0, 1, 0], [0, 0, 0, 0, 1]]), L[2],](images/exo3_57.gif)
![matrix([[1, 0, 0, 0, 0], [0, 1, 0, 0, 0], [0, 0, 1, 0, 0], [0, 0, 0, 1, 0], [0, 0, 0, 0, 1]]), L[1],](images/exo3_58.gif)
Donc:
| > | inv_A:=inverse(A); |
![inv_A := matrix([[1/2, 1/4, (-5)/12, (-2)/3, 3/4], [1/6, (-1)/12, (-7)/36, (-1)/9, 1/12], [(-1)/3, 1/6, (-5)/18, (-4)/9, 5/6], [(-1)/6, 7/12, 1/36, (-14)/9, 17/12], [(-1)/2, (-1)/4, 3/4, 1, (-3)/4]])](images/exo3_59.gif)
Méthode 2: appliqué à B, on résout le systéme associé
| > | Gsyst_cramer(B,[x,y,z,t],[a,b,c,d]); |

![L[1],](images/exo3_61.gif)
![L[2],](images/exo3_62.gif)
![L[3],](images/exo3_63.gif)
![L[4],](images/exo3_64.gif)
![L[2],](images/exo3_65.gif)
![L[3],](images/exo3_66.gif)
![L[4],](images/exo3_67.gif)
![L[3],](images/exo3_68.gif)
![L[4],](images/exo3_69.gif)
![L[4],](images/exo3_70.gif)
![L[2],](images/exo3_71.gif)
![L[3],](images/exo3_72.gif)
![L[1],](images/exo3_73.gif)
![L[2],](images/exo3_74.gif)
![L[1],](images/exo3_75.gif)
D'où
| > | inv_B:=inverse(B); |
![inv_B := matrix([[0, 0, 1/3, 1/3], [1/9, (-1)/9, (-1)/9, 0], [(-8)/9, (-1)/9, 5/9, 2/3], [(-10)/9, 1/9, 13/9, 1/3]])](images/exo3_76.gif)
| > | question c) |
la matrice canoniquement associée à phi est
| > | M:=matrix(5,4,[[1,0,1,0],[0,1,0,1],[1,0,0,1],[1,0,0,0],[0,1,0,0]]); |
![M := matrix([[1, 0, 1, 0], [0, 1, 0, 1], [1, 0, 0, 1], [1, 0, 0, 0], [0, 1, 0, 0]])](images/exo3_77.gif)
la matrice de passage de la base canonique de R4 à celle proposée est P=transposée(B)
| > | P:=transpose(B); |
![P := matrix([[2, 1, 1, 2], [1, -10, 2, -2], [-1, 0, -1, 1], [0, -1, 1, -1]])](images/exo3_78.gif)
| > | La matrice de passage de la base canonique de R5 à celle proposée est Q=transposée(A) |
| > | Q:=transpose(A); |
![Q := matrix([[2, 1, 1, 2, 2], [1, -10, 2, -2, 2], [-1, 0, -1, 1, 1], [0, -1, 1, -1, 0], [1, -2, 2, 1, 2]])](images/exo3_79.gif)
| > |
son inverse est donc Q^(-1)=transposée(A^(-1))
| > | inv_Q:=transpose(inv_A); |
![inv_Q := matrix([[1/2, 1/6, (-1)/3, (-1)/6, (-1)/2], [1/4, (-1)/12, 1/6, 7/12, (-1)/4], [(-5)/12, (-7)/36, (-5)/18, 1/36, 3/4], [(-2)/3, (-1)/9, (-4)/9, (-14)/9, 1], [3/4, 1/12, 5/6, 17/12, (-3)/4]])](images/exo3_80.gif)
On en déduit la matrice N relative aux nouvelles bases N=inv_Q * M * P
| > | N:=evalm(inv_Q&*M&*P); |
![N := matrix([[(-5)/6, 7/2, (-4)/3, 4/3], [17/12, 17/4, 1/6, 17/6], [(-13)/36, (-23)/4, 7/18, (-43)/18], [(-34)/9, -11, (-7)/9, (-65)/9], [55/12, 35/4, 11/6, 43/6]])](images/exo3_81.gif)
| > |