| > | restart; |
| > | with(plots);with(student); |
Warning, the name changecoords has been redefined
![]()
![]()
![]()
![]()
Exercice 25
question a)
| > | Dom:={ x>=0,y>=0,x^2/a^2+y^2/b^2<=1}; |

| > | f:=(x,y)-> (x^3+y^3); |
![]()
| > | a:=1:b:=2:implicitplot(Dom,x=-3..3,y=-3..3,thickness=3);a:='a':b:='b': |
![[Plot]](images/exo25_7.gif)
Changement de coordonnées affine
| > | u=a*x,v=b*y; |
![]()
| > | Doubleint('f'(u,v),u,v,A)= Doubleint('f'(a*x,b*y)*abs(a*b),x,y,C); |
![]()
Où le domaine d'intégration est le quart de cercle trigo C
| > | a:=1:b:=1:implicitplot(Dom,x=-2..2,y=-2..2,thickness=3);a:='a':b:='b': |
![[Plot]](images/exo25_10.gif)
Changement de coordonnées polaires
| > | Doubleint('f'(a*x,b*y),x,y,C)= Doubleint('f'(a*r*cos(theta),b*r*sin(theta))*abs(r),r,theta,Cpol); |
![]()
domaine d'intégration polaire
| > | inequal({r>=0,r<=1,theta<=Pi/2,theta>=0},r=-1..2,theta=-1..2,optionsexcluded=(color=white)); |
![[Plot]](images/exo25_12.gif)
| > | Doubleint(f(x,y),x,y,A)= Doubleint(simplify(f(a*r*cos(theta),b*r*sin(theta))*r),r=0..1,theta=0..Pi/2) ,"=",value( Doubleint(simplify(f(a*r*cos(theta),b*r*sin(theta))*r),r=0..1,theta=0..Pi/2)); |

| > | Doubleint('f'(u,v),u,v,A)=2*a*b/15*(a^3+b^3); |
![]()
question b)
| > | Dom:={y>=0, x*x+y*y<=2*x}; |
![]()
| > | f:=(x,y)->x^2*y; |
![]()
| > | implicitplot(Dom,x=0..2,y=-1..1,thickness=3); |
![[Plot]](images/exo25_17.gif)
Changement de coordonnées polaires
| > | Doubleint('f'(x,y),x,y,A)= Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r,theta,Apol); |
![]()
domaine d'intégration polaire Apol
| > | Dpol:={0<=theta,theta<=Pi/2,0<=r,r<=2*cos(theta)}; |
![]()
| > | implicitplot(Dpol,r=0..2,theta=0..1.55,thickness=3); |
![[Plot]](images/exo25_20.gif)
| > | Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r,theta,Apol)= Doubleint(f(r*cos(theta),r*sin(theta))*abs(r),r=0..2*cos(theta),theta=0..Pi/2) ,"=",value( Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r=0..2*cos(theta),theta=0..Pi/2) ); |

question c)
| > | Dom:={x>=1, x*x+y*y<=2*x}; |
![]()
| > | f:=(x,y)->1/(x^2+y^2)^2; |
![]()
| > | implicitplot(Dom,x=0..2,y=-1..1,thickness=3); |
![[Plot]](images/exo25_24.gif)
Changement de coordonnées polaires
| > | Doubleint('f'(x,y),x,y,A)= Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r,theta,Apol); |
![]()
domaine d'intégration polaire Apol
| > | Dpol:={-Pi/4<=theta,theta<=Pi/4,1/cos(theta)<=r,r<=2*cos(theta)}; |
![]()
| > | implicitplot(Dpol,r=0..2,theta=-0.77..0.77,thickness=3); |
![[Plot]](images/exo25_27.gif)
| > | Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r,theta,Apol)= Doubleint(simplify(f(r*cos(theta),r*sin(theta))*r),r=1/cos(theta)..2*cos(theta),theta=-Pi/4..Pi/4) ,"=",value( Doubleint(f(r*cos(theta),r*sin(theta))*r,r=1/cos(theta)..2*cos(theta),theta=-Pi/4..Pi/4) ); |

question d)
| > | Dom:={x>=0,y>=0, x*x+y*y>=2*y,x*x+y*y<=1}; |
![]()
| > | f:=(x,y)->sqrt(x^2+y^2); |
![]()
| > | implicitplot(Dom,x=0..1,y=0..1,thickness=3); |
![[Plot]](images/exo25_31.gif)
Changement de coordonnées polaires
| > | Doubleint('f'(x,y),x,y,A)= Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r,theta,Apol); |
![]()
domaine d'intégration polaire Apol
| > | Dpol:={0<=theta,theta<=Pi/6,2*sin(theta)<=r,r<=1}; |
![]()
| > | implicitplot(Dpol,r=0..1,theta=0..0.52,thickness=3); |
![[Plot]](images/exo25_34.gif)
| > | Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r,theta,Apol)= Doubleint(simplify(f(r*cos(theta),r*sin(theta))*r),r=2*sin(theta)..1,theta=0..Pi/6) ,"=",value( Doubleint(simplify(f(r*cos(theta),r*sin(theta))*r),r=2*sin(theta)..1,theta=0..Pi/6) ); |

| > |
| > |
| > | question e) |
| > | Dom:={(x-1)^2+y^2<=1}; |
![]()
| > | f:=(x,y)->x^2-y^2; |
![]()
| > | implicitplot(Dom,x=-1..2,y=-2..2,thickness=3); |
![[Plot]](images/exo25_38.gif)
Changement de coordonnées polaires
| > | Doubleint('f'(x,y),x,y,A)= Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r,theta,Apol); |
![]()
domaine d'intégration polaire Apol
| > | Dpol:={-Pi/2<=theta,theta<=Pi/2,0<=r,r<=2*cos(theta)}; |
![]()
| > | implicitplot(Dpol,r=0..2,theta=-1.52..1.52,thickness=3); |
![[Plot]](images/exo25_41.gif)
| > | Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r,theta,Apol)= Doubleint(simplify(f(r*cos(theta),r*sin(theta))*r),r=0..2*cos(theta),theta=-Pi/2..Pi/2) ,"=",value( Doubleint(simplify(f(r*cos(theta),r*sin(theta))*r),r=0..2*cos(theta),theta=-Pi/2..Pi/2)); |

question f)
| > | Dom:={ x^2+y^2<=R*x}; |
![]()
| > | f:=(x,y)-> sqrt(R^2-(x^2+y^2)); |
![]()
| > | R:=2:implicitplot(Dom,x=-3..3,y=-3..3,thickness=3);R:='R': |
![[Plot]](images/exo25_45.gif)
Changement de coordonnées polaires
| > | Doubleint('f'(x,y),x,y,A)= Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r,theta,Apol); |
![]()
domaine d'intégration polaire Apol
| > | Dpol:={-Pi/2<=theta,theta<=Pi/2,0<=r,r<=R*cos(theta)}; |
![]()
| > | R:=2:implicitplot(Dpol,r=0..2,theta=-1.52..1.52,thickness=3);R:='R':assume(R>0): |
![[Plot]](images/exo25_48.gif)
| > | Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r,theta,Apol)= Doubleint(simplify(f(r*cos(theta),r*sin(theta))*r),r=0..R*cos(theta),theta=-Pi/2..Pi/2) ,"=",value( Doubleint(simplify(f(r*cos(theta),r*sin(theta))*r),r=0..R*cos(theta),theta=-Pi/2..Pi/2)); |
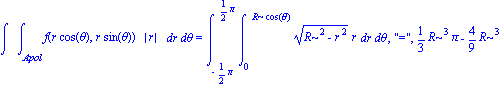
| > |