| > | restart; |
| > | with(plots);with(student); |
Warning, the name changecoords has been redefined
![]()
![]()
![]()
![]()
Exercice 26
question a)
| > | Dom:={ x>=0,y>=0,x^2+y^2<=1,x<=x^2+y^2}; |
![]()
| > | f:=(x,y)-> x+y; |
![]()
| > | implicitplot(Dom,x=0..1,y=0..1,thickness=3); |
![[Plot]](images/exo26_7.gif)
Changement de coordonnées polaires
| > | Doubleint('f'(x,y),x,y,A)= Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r,theta,Apol); |
![]()
domaine d'intégration polaire
| > | Dpol:={0<=theta,theta<=Pi/2,cos(theta)<=r,r<=1}; |
![]()
| > | implicitplot(Dpol,r=0..0.995,theta=0..1.55,thickness=3); |
![[Plot]](images/exo26_10.gif)
| > | Doubleint('f'(x,y),x,y,A)= Doubleint('f'(r*cos(theta),r*sin(theta))*r,r=cos(theta)..1,theta=0..Pi/2) ,"=",Doubleint(simplify(f(r*cos(theta),r*sin(theta))*r),r=cos(theta)..1,theta=0..Pi/2) ,"=",value( Doubleint(f(r*cos(theta),r*sin(theta))*r,r=cos(theta)..1,theta=0..Pi/2) ); |

question b)
| > | Dom:={ y>=0,x^2+y^2<=x,y<=x^2+y^2}; |
![]()
| > | f:=(x,y)-> x^2+y^2; |
![]()
| > | implicitplot(Dom,x=0..1,y=0..0.5,thickness=3); |
![[Plot]](images/exo26_14.gif)
Changement de coordonnées polaires
| > | Doubleint('f'(x,y),x,y,A)= Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r,theta,Apol); |
![]()
domaine d'intégration polaire
| > | Dpol:={0<=theta,theta<=Pi/4,sin(theta)<=r,r<=cos(theta)}; |
![]()
| > | implicitplot(Dpol,r=0..1,theta=0..0.75,thickness=3); |
![[Plot]](images/exo26_17.gif)
| > | Doubleint('f'(x,y),x,y,A)= Doubleint('f'(r*cos(theta),r*sin(theta))*r,r=sin(theta)..cos(theta),theta=0..Pi/4) ,"=",Doubleint(simplify(f(r*cos(theta),r*sin(theta))*r),r=sin(theta)..cos(theta),theta=0..Pi/4) ,"=",value( Doubleint(f(r*cos(theta),r*sin(theta))*r,r=sin(theta)..cos(theta),theta=0..Pi/4) ); |

| > |
question c)
| > | Dom:={ (x^2+y^2)^2<=2*x*y}; |
![]()
| > | f:=(x,y)-> sqrt(x*y); |
![]()
| > | implicitplot(Dom,x=-1..1,y=-1..1,thickness=3); |
![[Plot]](images/exo26_21.gif)
puisque le domaine d'intégration est symétrique par rapport à O et que
| > | 'f'(-x,-y)='f'(x,y); |
![]()
On a
| > | Doubleint('f'(x,y),x,y,A)= 2 *Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r,theta,B); |
![]()
Où B est la partie de A dont les abscisses sont positives
| > | DomB:={ (x^2+y^2)^2<=2*x*y,x>=0}; |
![]()
| > | implicitplot(Dom,x=0..1,y=-1..1,thickness=3); |
![[Plot]](images/exo26_25.gif)
Changement de coordonnées polaires
| > | Doubleint('f'(x,y),x,y,B)= Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r,theta,Bpol); |
![]()
domaine d'intégration polaire
| > | Dpol:={0<=theta,theta<=Pi/2,r^2<=sin(2*theta)}; |
![]()
| > | implicitplot(Dpol,r=0..1,theta=-1.52..1.57,thickness=3); |
![[Plot]](images/exo26_28.gif)
| > |
| > |
| > | Doubleint('f'(x,y),x,y,B)= Doubleint('f'(r*cos(theta),r*sin(theta))*r,r=0..sqrt(sin(2*theta)),theta=0..Pi/2) ,"=",Doubleint(simplify(f(r*cos(theta),r*sin(theta))*r),r=0..sqrt(sin(2*theta)),theta=0..Pi/2) ,"=",value( Doubleint(f(r*cos(theta),r*sin(theta))*r,r=0..sqrt(sin(2*theta)),theta=0..Pi/2) ); |

| > | Doubleint('f'(x,y),x,y,A)=2*1/24*2^(1/2)*Pi; |
![]()
question d)
| > | Dom_polaire:={ abs(r)<=sqrt(cos(theta))}; |
![]()
| > | f:=(x,y)-> x^2; |
![]()
| > | implicitplot(Dom_polaire,r=-1..1,theta=-Pi/2..Pi/2,thickness=3); |
![[Plot]](images/exo26_33.gif)
Changement de coordonnées polaires
| > | Doubleint('f'(x,y),x,y,A)= Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r,theta,Apol); |
![]()
| > | Doubleint('f'(x,y),x,y,A)= Doubleint('f'(r*cos(theta),r*sin(theta))*abs(r),r=-sqrt(cos(theta))..sqrt(cos(theta)),theta=-Pi/2..Pi/2) ,"=",Doubleint(simplify(f(r*cos(theta),r*sin(theta))*abs(r)),r=-sqrt(cos(theta))..sqrt(cos(theta)),theta=-Pi/2..Pi/2) ,"=",value( Doubleint(f(r*cos(theta),r*sin(theta))*abs(r),r=-sqrt(cos(theta))..sqrt(cos(theta)),theta=-Pi/2..Pi/2) ); |

| > |
question e)
| > | Dom:={ x>=0,y>=0,x+y<=1}; |
![]()
| > | f:=(x,y)-> (x+y)^2*exp(x^2-y^2);; |
![]()
| > | inequal(Dom,x=-1..2,y=-1..2,optionsexcluded=(color=white)); |
![[Plot]](images/exo26_38.gif)
Changement de coordonnées affine
| > | u=x+y,v=x-y; |
![]()
| > | Doubleint('f'((u+v)/2,(u-v)/2),u,v,B)= Doubleint('f'(x,y)*abs(2),x,y,A); |

Où le domaine d'intégration est le quart de cercle trigo C
| > | DomB:={ u+v>=0,u-v>=0,u<=2}; |
![]()
| > | inequal(DomB,u=-1..2,v=-2..2,optionsexcluded=(color=white)); |
![[Plot]](images/exo26_42.gif)
| > | Doubleint('f'(x,y),x,y,A)=1/2*Doubleint('f'((u+v)/2,(u-v)/2),v=-u..u,u=0..1),"=",1/2*Doubleint(simplify(f((u+v)/2,(u-v)/2)),v=-u..u,u=0..1),"=",value(1/2*Doubleint(f((u+v)/2,(u-v)/2),v=-u..u,u=0..1)) ; |
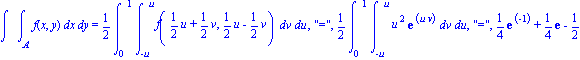
question f)
| > | Dom:={ x*y>=1,y>=x,x+y>=0,x+y<=4}; |
![]()
| > | f:=(x,y)-> (x^2-y^2)*cos(x*y);; |
![]()
| > | implicitplot(Dom,x=0..4,y=-1..4,thickness=3); |
![[Plot]](images/exo26_46.gif)
Changement de coordonnées affine
| > | u=x+y,v=x-y; |
![]()
| > | Doubleint('f'((u+v)/2,(u-v)/2),u,v,B)= Doubleint('f'(x,y)*abs(2),x,y,A); |

Où le domaine d'intégration est le quart de cercle trigo C
| > | DomB:={ (u+v)*(u-v)>=1,u-v>=u+v,u<=4,u>=0}; |
![]()
| > | implicitplot(DomB,u=0..4,v=-4..0,thickness=3); |
![[Plot]](images/exo26_50.gif)
| > | Doubleint('f'(x,y),x,y,A)=1/2*Doubleint('f'((u+v)/2,(u-v)/2),v=-sqrt(u^2-4)..0,u=2..4),"=",1/2*Doubleint(simplify(f((u+v)/2,(u-v)/2)),v=-sqrt(u^2-4)..0,u=2..4),"=",value(1/2*Doubleint(f((u+v)/2,(u-v)/2),v=-sqrt(u^2-4)..0,u=2..4)) ; |

| > |