| > | restart;with(linalg); |
Warning, the protected names norm and trace have been redefined and unprotected
![]()
![]()
![]()
![]()
| > |
| > |
| > | Evaluation 6 |
| > |
question a)
| > | P:=matrix(3,3,[[2,4,3],[0,1,1],[2,2,-1]]); |
![P := matrix([[2, 4, 3], [0, 1, 1], [2, 2, -1]])](images/eval06_5.gif)
Pour calculer l'inverse on étudie le sytème associé
| > | Gsyst_cramer(P,[x1,x2,x3],[y1,y2,y3]); |
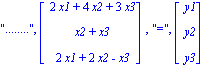
![L[1],](images/eval06_7.gif)
![L[3],](images/eval06_8.gif)
![L[3],](images/eval06_9.gif)
![L[3],](images/eval06_10.gif)
![L[1],](images/eval06_11.gif)
![L[2],](images/eval06_12.gif)
![L[1],](images/eval06_13.gif)
On en déduit l'inverse de P
| > | inv_P:=inverse(P); |
![inv_P := matrix([[3/4, (-5)/2, (-1)/4], [(-1)/2, 2, 1/2], [1/2, -1, (-1)/2]])](images/eval06_14.gif)
Autre méthode: on mène en paraallèle le pivot de Gauss partant de P et de I_3
| > | Ginverse(P); |
![matrix([[2, 4, 3], [0, 1, 1], [2, 2, -1]]),](images/eval06_15.gif)
![matrix([[1, 2, 3/2], [0, 1, 1], [2, 2, -1]]), L[1],](images/eval06_16.gif)
![matrix([[1, 2, 3/2], [0, 1, 1], [0, -2, -4]]), L[3],](images/eval06_17.gif)
![matrix([[1, 2, 3/2], [0, 1, 1], [0, 0, -2]]), L[3],](images/eval06_18.gif)
![matrix([[1, 2, 3/2], [0, 1, 1], [0, 0, 1]]), L[3],](images/eval06_19.gif)
![matrix([[1, 2, 0], [0, 1, 1], [0, 0, 1]]), L[1],](images/eval06_20.gif)
![matrix([[1, 2, 0], [0, 1, 0], [0, 0, 1]]), L[2],](images/eval06_21.gif)
![matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]]), L[1],](images/eval06_22.gif)
| > | question b) |
| > | la matrice de phi dans la base canonique est |
| > | M:=matrix(3,3,[[2,1,1],[3,0,-1],[-1,1,1]]); |
![M := matrix([[2, 1, 1], [3, 0, -1], [-1, 1, 1]])](images/eval06_23.gif)
la matrice de passage Q de l'ancienne à la nouvelle base est la transposée de P (voir question a))
| > | Q:=transpose(P); |
![Q := matrix([[2, 0, 2], [4, 1, 2], [3, 1, -1]])](images/eval06_24.gif)
on en déduit l'inverse de Q, comme étant la transposée de l'inverse de P
| > | inv_Q:=transpose(inv_P); |
![inv_Q := matrix([[3/4, (-1)/2, 1/2], [(-5)/2, 2, -1], [(-1)/4, 1/2, (-1)/2]])](images/eval06_25.gif)
D'où la matrice M_prime dans la nouvelle base
| > | M_prime:=evalm(inv_Q&*M&*Q); |
![M_prime := matrix([[37/4, 3, (-1)/4], [(-53)/2, -9, 5/2], [(-15)/4, -2, 11/4]])](images/eval06_26.gif)
| > | question c) |
| > | u:=vector([1,1,1]); |
![]()
| > | a:=Pi/3; |
![]()
| > | n:=vector([1,-1,1]); |
![]()
| > | n_normé:=evalm(n/sqrt(3)); |
![]()
on note u_n le projeté orthogonal de u sur Vect(n)
| > | u_n:=evalm(innerprod(u,n_normé)*n_normé); |
![]()
| > |
| > | on note u_p le projeté orthogonal de u sur l'orthogonal de Vect(n) |
| > | u_p:=evalm(u-u_n); |
![]()
la rotation de u_p donne v_p= cos(a) u_p+ sin(a)( n_normé vectoriel u_p)
| > | v_p:=evalm(cos(a)*u_p+ sin(a)*crossprod( n_normé,u_p)); |
![]()
Enfin puisque u_n est invariant par rotation:
| > | Rot(u)=evalm(v_p+u_n); |
![]()
| > | question d) |
| > | S:=matrix(3,3,[[16,4,4],[-4,17,-1],[4,1,1]]);a:='a': |
![S := matrix([[16, 4, 4], [-4, 17, -1], [4, 1, 1]])](images/eval06_35.gif)
| > | Gsyst(S,[x,y,z],[0,a^2,a+a^2]); |
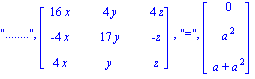
![L[1],](images/eval06_37.gif)
![L[2],](images/eval06_38.gif)
![L[3],](images/eval06_39.gif)
![L[2],](images/eval06_40.gif)
![]()
![]()
![]()
![]()
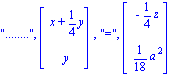
![L[1],](images/eval06_46.gif)
On en déduit, pas de solutions si a est different de 0 ou -1
Si a=1
| > | S_1= vector([-1/72,1/18,0])+R*vector([-1/4,0,1]); |
![]()
Si a=0
| > | S_0= R*vector([-1/4,0,1]); |
![]()
| > | question e) |
| > | A:=-1/9*matrix([[7,4,4],[-4,8,-1],[4,1,-8]]); |
![A := -1/9*matrix([[7, 4, 4], [-4, 8, -1], [4, 1, -8]])](images/eval06_49.gif)
A est orthognale car t(A)A=I_3
| > | tAA:=evalm(transpose(A)&*A); |
![tAA := matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]])](images/eval06_50.gif)
A est dans SO(3) car son déterminant vaut
| > | determinant_A:=det(A); |
![]()
On calcule l'ensemble des invariants en étudiant le systeme AX=X où X est le vecteur colonne [x,y,z] des coordonnée d'un vecteur de R3
| > | Gsyst(A-matrix([[1,0,0],[0,1,0],[0,0,1]]),[x,y,z],[0,0,0]); |
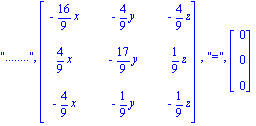
![L[1],](images/eval06_53.gif)
![L[2],](images/eval06_54.gif)
![L[3],](images/eval06_55.gif)
![L[2],](images/eval06_56.gif)
![]()
![]()
![]()
![]()
![L[1],](images/eval06_62.gif)
On retrouve comme calculé dans la question précédente,
| > | Inv_A=R*k;k:=evalm(vector([1,0,-4])/sqrt(17)); |
![]()
![]()
Il s'agit d'une rotation autour de k
on choisit a unitaire, orthogonal à k, par exemple
| > | a:=vector([0,1,0]); |
![]()
on a normalisé le vecteur k ce qui nous permet de caractériser l'angle t de la rotation
| > | cosinus:=innerprod(a,A&*a); |
![]()
| > | sinus:=innerprod(crossprod(a,A&*a),k); |
![]()
| > |